 dość nieprecyzyjne, nieczytelne, jak dlamń, sformuowanie pytania. ale tak jak zrozumiałem tak
zrobimy
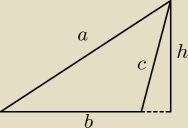
tworzymy sobie, Waćpanna, funkcję dwóch zmiennych, czyli po polsku piszemy wzór na pole
trójkąta.
Za pomocą podanych jeszcze zależności(że ich suma ma 16 jednostek) pozbywamy się jednej
niewiadomej
b+h=16 P(h,b)=1/2*b*h ⇔ b=16−h ⇔P(h)=1/2*(16−h)h
P(h)= −1/2*h2 + 8h
mamy, proszę Nadobna, funkcję kwadratową prezentującą nam pole tegoż trójkąta w zależności od
wysokości ów trójkąta. Mamy wyliczyć wysokość przy największym polu trójkąta.
postępujemy jak przy funkcji kwadratowej − ma ona ramiona w dół, bo jest ujemny współczynnik
przy h o najwyższej potędze (−1/2) więc największą jej wartością będzie wartość xwierzchołka
= −B2A z czego A=−1/2 i B =8
xwierzchołka=16, co jest naszą wysokością przy maksymalnym polu, o Mości Panienko. Tadam
dość nieprecyzyjne, nieczytelne, jak dlamń, sformuowanie pytania. ale tak jak zrozumiałem tak
zrobimy
tworzymy sobie, Waćpanna, funkcję dwóch zmiennych, czyli po polsku piszemy wzór na pole
trójkąta.
Za pomocą podanych jeszcze zależności(że ich suma ma 16 jednostek) pozbywamy się jednej
niewiadomej
b+h=16 P(h,b)=1/2*b*h ⇔ b=16−h ⇔P(h)=1/2*(16−h)h
P(h)= −1/2*h2 + 8h
mamy, proszę Nadobna, funkcję kwadratową prezentującą nam pole tegoż trójkąta w zależności od
wysokości ów trójkąta. Mamy wyliczyć wysokość przy największym polu trójkąta.
postępujemy jak przy funkcji kwadratowej − ma ona ramiona w dół, bo jest ujemny współczynnik
przy h o najwyższej potędze (−1/2) więc największą jej wartością będzie wartość xwierzchołka
= −B2A z czego A=−1/2 i B =8
xwierzchołka=16, co jest naszą wysokością przy maksymalnym polu, o Mości Panienko. Tadam
| −8 | ||
chochlik trochę w końcówce namieszał, xw = | = 8 | |
| −1 |

