help! Wydi: Wyznacz równanie okręgu, który jest obrazem okręgu (x+4)²+(y−7)²=27 w jednokładności o środku S(−1;4) i skali 1/3

Wydi:

Wydi: ponawiam

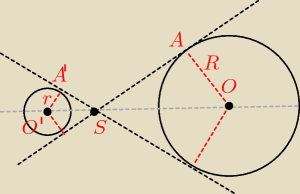
Jack: O(−4,7) S(−1,4) Z podobieństwa trójkątów O'A'S oraz OAS (cecha kkk) można pokazać, że r=¹₃R. ponadto z tego samego podobieństwa mamy: |SO'|=¹₃|SO| Policz długość |SO|, oblicz równanie prostej przechodzącej przez punkty S i O, zbuduj wektor równoległy do niej, nadaj mu długość ¹₃|SO| i przesuń punkt S o ten wektor a otrzymasz punkt O'.

Wydi: A więc: 1) długość ISOI SO=√(−4+1)²+(7−4)²=√18=3√2 2)prosta przechodząca przez pkt S i O. 4=−a+b 7=−4a+b −4=a−b 7=−4a+b 3=−3a −1=a 4=1+b 3=b czyli a=−1 i b=3 więc y=−x+3

Wydi: 3)prosta równoległa do y=−x+3 to y=−x+b

Jack: ok, prosta y+x−3=0, czyli wektor "w" równoległy do prostej ma postać [−1,1] (lub [1,−1]). sprawdźmy czy: w'+ S = O, gdzie w' to wektor w tym samym kierunku co w, ale o długości 3√2. Ustalamy długość wektora w'. Wektor w'=a*[−1,1]=[−a,a] ma mieć długość 3√2 ("a" to skalar). √(−a)²+a²=3√2 / ² 2a²=18 a=±3 Zatem nasz wektor w'= [−3,3] lub w'= [3,−3]. Jeśli weźmiemy ten pierwszy otrzymamy: S+w'=O (−1,−4)+ [−3,3]= (−4,7) (−4,7)=(−4,7) L=P czyli sprawdziliśmy że faktycznie wektor został dobrze dobrany. Na tej samej zasadzie podamy współrzędną punktu O'. (właściwa część zadania ) Weźmy wektor [1,−1] i nadajmy mu długość ¹₃ * 3√2=√2 zatem 2a²=2, a=±1. Zatem weźmy [1,−1]. (Zauważmy że musi mieć zwrot przeciwny do wektora, który użyliśmy do wyznaczenia punktu O). czyli [1,−1]+ S = O' [1,−1]+(−1,4)=O' (0,3)=O' Czy okrąg ma równanie x²+(y−3)²=2

Wydi: dzięki za pomoc