planimetria sylwester: Najkrótszy bok trapezu równoramiennego ma długość równą długości promienia okręgu weń wpisanego Wyznacz tangens kąta ostrego trapezu. Proszę o pomoc

*: ?

blabla: Potrafi to ktoś rozwiązać?

Janek191: b = r a > b b, a − długości podstaw trapezu równoramiennego

	r		a
c =		+
	2		2

c − długość ramienia trapezu h = 2 r − wysokość trapezu

	a		r
x =		−
	2		2

Z tw. Pitagorasa mamy x² + h² = c² czyli

	a		r		r		a
[		−		]2 + ( 2r)2 = [		+		]2
	2		2		2		2

a2		a*r		r2		r2		a*r		a2
	−		+		+ 4 r2 =		+		+
4		2		4		4		2		4

a*r = 4 r² / : r a = 4 r =====

	2 r		2 r		4r		4r
tg α =		=		=		=		=
	x		0,5 *( a − r)		a − r		4r − r

	4r		4
=		=
	3r		3

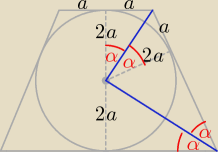
Bogdan: albo tak:

	a		1
tgα =		=
	2a		2

	2tgα		1   2*   2		1		4
tg(2α) =		=		=		=
	1 − tg2α		1   1 −   4		3   4		3

blabla: dziękuje

wojtek: Jak Bogdan obliczył tg(2α)? skąd ten wzór po znaku równości?

wojtek: up. nurtuje mnie to, nie wiem jak do tego dojsc.

wojtek:

	1
samemu doszedłem do tego, że z tabelki można odczytać najbliższy kąt tgα dla		, czyli
	2

27stopni, pomnożyć razy 2, i odczytać ile wynosi dla 54stopni, czyli 1,3764. jednakże nie jest to wynik taki ładny jak u Bogdana. czekam na jakiegoś samarytanina, albo samarytankę.

Eta:

	sin2α		2sinα*cosα
tg2α=		=		=
	cos2α		cos2α−sin2α

	2sinαcosα   cos2α		2tgα
=		=
	cos2α−sin2α   cos2α		1−tg2α

wojtek: dziękuję Ci, o miłosierna

1234: Bogdan. A skąd wiemy że te dwa kąty przy środku okręgu równają sie α ? Mógłbyś mi to wytlumaczyć?