zad
matthew: Cześć, mam takie zadanie:
w układzie współrzędnych narysuj okrąg o równaniu (x+2)2 + (y−3)2 = 4 oraz zaznacz punkt
A=(0,4). Prosta o równaniu x = 0 jest jedną ze stycznych do tego okręgu przechodzących przez
punkt A. Wyznacz równanie drugiej stycznej do tego okręgu, przechodzącej przez punkt A.
Czy tutaj należy wyznaczyć wzór tej stycznej, "wyglądałby on chyba tak: y = ax −1", a potem
wstrawić go w miejsce y do równania na okrag? wiem ze Δ=0 aby istniała stycznośc...
proszę o pomoc
5 kwi 20:03
matthew: Mam jeszcze takie zadanie:
Dany jest ostrosłup prawidłowy trójkatny, w którym krawędź podstawy ma długość a i krawędź
boczna jest od niej dwa razy dłuższa. Oblicz cosunus kąta między krawędzią boczną i krawędzią
podstawy ostrosłupa. Narysuj przekrój ostrosłupa płaszczyzna przechodzącą przez krawędź
podstawy i środek przeciwległej krawędzi bocznej i oblicz pole tego przekroju.
Zacząłem ta pierwsza cześć zadania:
(2a)
2 = a
2 + (2a)
2 − 2a(2a)cosα
4a
2 = a
2 + 4a
2 − 4a
2cosα
4a
2cosα = a
2
Bardzo prosze o sprawdzenie...
Nie jestem pewien jak narysować rysunek dotyczący drugiej części zadania....
Jeśli ktoś może go narysowac, to bardzo bym prosil
z góry dziękuję

5 kwi 20:28
matthew: aha i ten cosinus w konsekwencji miałby 45o ?
5 kwi 20:29
Godzio: pomagam
5 kwi 21:06
Wydi: Z tego co widzę po zadaniach to panowie prawdopodobnie zdają rozszerzoną mate w tym roku na
maturce

5 kwi 21:21
Godzio:
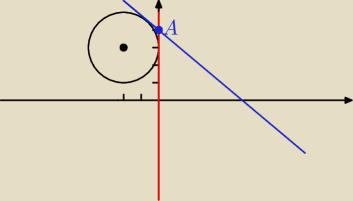
y = ax + b
prosta przechodzi przez (0,4) wiec:
b = 4
Nasza prosta ma postać:
y = ax + 4
(x+2)
2 + (y−3)
2 = 4
(x+2)
2 + (ax + 1)
2 = 4
x
2 + 4x + 4 + a
2x
2 + 2ax + 1 = 4
(1+a
2)x
2 + (4+2a)x + 1 = 0
Δ = 0
16 + 16a + 4a
2 − 4 − 4a
2 = 0
16a = −12
5 kwi 21:21
matthew: Godzio ja tam się pomyliłem.... tam powinno być A=(0, −1) ale jest ok

czyli tak jak
myślałem tylko, ze robiłem bład w rachunkach....
dzięki

5 kwi 21:48
matthew: a możesz zobaczyć to drugie zadanie?
5 kwi 21:49
paziówna: | | 1 | |
ja zobacze  jesli cosα = |
| to watpliwe, zeby α = 45 o...  przeciez wtedy cosα = |
| | 4 | |
5 kwi 21:54
Godzio:
coś nie mogę wpaść na rozwiązanie
5 kwi 21:56
paziówna:
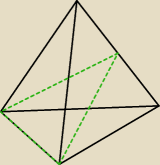
5 kwi 21:57
paziówna: a z rysunkiem dasz sobie rade?

5 kwi 21:57
paziówna: tzn majac rysunek, czy dasz sobie rade z zadaniem?

5 kwi 21:58
matthew: nie wiem, chyba bedzie ciezko

| | √2 | | 1 | |
no jasne, ze tak cos 45o to |
| , ale w takim razie jak przekształcić cos |
| na kąt |
| | 2 | | 4 | |
5 kwi 22:04
Godzio: Masz może wynik bo wyszło mi :
5 kwi 22:07
Godzio: taki kąt to jedynie w tablicach mozna sprawdzic

ale ty masz w poleceniu "Oblicz cos" a nie
"Oblicz kat"
5 kwi 22:09
matthew: nie, niestety nie mam odpowiedzi

ok ale ogolnie z tym cosinusem jest dobrze ?
5 kwi 22:12
Godzio: tak
5 kwi 22:12
Godzio:
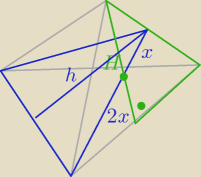
Dam moje rozwiązanie
H
2 = 4a
2 − 0,25a
2
| | 1 | | 1 | |
(2x)2 = ( |
| H)2 + |
| a2 |
| | 3 | | 4 | |
| | 1 | | 15 | | 1 | |
4x2 = |
| * |
| a2 + |
| a2 |
| | 9 | | 4 | | 4 | |
to 2x i x => środkowa dzieli się w stosunku 1:2
Jak czegoś nie rozumiesz to pisz
5 kwi 22:13
5 kwi 22:32


 y = ax + b
prosta przechodzi przez (0,4) wiec:
b = 4
Nasza prosta ma postać:
y = ax + 4
(x+2)2 + (y−3)2 = 4
(x+2)2 + (ax + 1)2 = 4
x2 + 4x + 4 + a2x2 + 2ax + 1 = 4
(1+a2)x2 + (4+2a)x + 1 = 0
Δ = 0
16 + 16a + 4a2 − 4 − 4a2 = 0
16a = −12
y = ax + b
prosta przechodzi przez (0,4) wiec:
b = 4
Nasza prosta ma postać:
y = ax + 4
(x+2)2 + (y−3)2 = 4
(x+2)2 + (ax + 1)2 = 4
x2 + 4x + 4 + a2x2 + 2ax + 1 = 4
(1+a2)x2 + (4+2a)x + 1 = 0
Δ = 0
16 + 16a + 4a2 − 4 − 4a2 = 0
16a = −12
 czyli tak jak
myślałem tylko, ze robiłem bład w rachunkach....
dzięki
czyli tak jak
myślałem tylko, ze robiłem bład w rachunkach....
dzięki
 jesli cosα =
jesli cosα =  przeciez wtedy cosα =
przeciez wtedy cosα =
 coś nie mogę wpaść na rozwiązanie
coś nie mogę wpaść na rozwiązanie




 ale ty masz w poleceniu "Oblicz cos" a nie
"Oblicz kat"
ale ty masz w poleceniu "Oblicz cos" a nie
"Oblicz kat"
 ok ale ogolnie z tym cosinusem jest dobrze ?
ok ale ogolnie z tym cosinusem jest dobrze ?
 Dam moje rozwiązanie
H2 = 4a2 − 0,25a2
Dam moje rozwiązanie
H2 = 4a2 − 0,25a2