jakie jest prawdopodobieństwo wylosowania białych kul smerfetka: jakie jest prawdopodobieństwo wylosowania 2 kul białych maruda: jakie jest prawdopodobieństwo wylosowania 2 kul białych.2 kul różnokolorowych maruda: z urny zawierającej 6 kul czarnych i 4 białe losujemy kolejno bez zwracania dwie kule.Jakie jest prawdopodobieństwo wylosowania.a)2kul białych..b)2 kul różnokolorowych.Rachunek prawdopodobieństwa

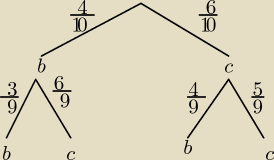
Nikka: b − biała c − czarna A − 2 kule białe

	4		3		2
P(A) =		8		=
	10		9		15

B − dwie kule różnego koloru

	4		6		6
P(B) =		*		+		*{4}{9} = ...
	10		9		10

mam nadzieję, że rozwiązanie jest ok

Nikka: poprawka

	4		3		2
P(A) =		*		=
	10		9		15

	4		6		6		4
P(B) =		*		+		*		= ...
	10		9		10		9

Gustlik: Nikka − kombinacjami jest prościej niż drzewkami. Drzewka są dobre tam, gdzie jest dwuetapowe doświadczenie, np.I etap − wybór urny, II etap − losowanie kul z urny. Przy zadaniach z losowaniem kul z urny, kart z talii itp. kombinatoryka jest zdecydowanie lepsza i szybsza od drzewek.

	10!
|Ω| = C102 =		= 45
	2!*8!

A − 2 kule białe

	4!
|A| = C42 =		= 6
	2!*2!

	6		2
P(A} =		=
	45		15

B − 2 kule różne |B| = C₄¹*C₆¹ = 4*6 = 24 (przy losowaniu elementów różnego rodzaju, np. różnych kul obowiązuje reguła mnożenia)

	24		8
P(B) =		=		.
	45		15

Nikka: wyobraź sobie, że dla mnie o wiele łatwiej jest drzewkiem

Nikka: nie widzę 'lepszości' Twojego rozwiązania... i ile liczenia, zastanawiania się czy to kombinacja, wariacja, itp. (a nie każdy potrafi rozróżniać), pojęcie silni, itp. − i w czym to niby prostsze, krótsze... każdy poprawny sposób jest dobry

Gustlik: Z liczeniem nie pa problemu − silnie ładnie się skraca i wychodzi mnożenie prostych liczb − z tym nie ma problemu, tym bardziej, że na maturze można mieć prosty kalkulator, a taki posiada mnożenie. Rozróżnić wariacje od kombinacji czy permutacji jest bardzo prosto: Permutacje − stosujesz tam, gdzie masz mozliwość poustawiania na różne sposoby n elementów w szeregu, np. książek na pólce, uczniow danej klasy w jednym rzędzie na apelu szkolnym itp. Wzór jest taki: P_n = n! Kombinacje − stosujesz przy losowaniu k elementów spośród n, przy czym kolejność losowanych elementów nie ma znaczenia, np. losowanie 3−osobowej delegacji z 30−osobowej klasy − C₃0³, losowanie 4 nieponumerowanych kul z 10 − C₁0⁴, LOTTO − losowanie 6 liczb z 49 − C₄9⁶ itp. Wzór jest taki:

	n k		n!		49 6		49!
Cnk =		=		, np. dla LOTTO będzie C496 =		=		, a
			k!*(n−k)!				6!*43!

silnie się ładnie skraca. Wariacje z powtórzeniami − stosujesz tam, gdzie kolejnośc losowania ma znaczenie, a losowane elementy mogą się powtarzać, np. 2−krotny rzut kostką − możesz otrzymać dwie różne liczby oczek, np. (1, 2), a możesz otrzymać np. dwie jedynki − dlatego z powtórzeniami − liczysz W₆², innym przykładem moze być losowanie ponumerowanych kul z urny ze zwracaniem − np. przy 3−krotnym losowaniu możesz wyciągnąć nawet 3 razy tę sama kulę, a mozesz za każdym razem inną. Wzór jest taki: W_n^k = n^k, np. dla rzutu dwiema kostkami będzie W₆² = 6² = 36. Wariacje bez powtórzeń − są podobne do tych z powtórzeniami, z tą tylko różnicą, że losowane elementy nie mogą się powtarzać. Przykładem może być losowanie kul z urny bez zwracania − wówczas za każdym razem wyciągniesz inną kulę, bo wylosowana wcześniej została odłozona na bok. Wzór jest taki:

	n!
Vnk =
	(n−k)!

Naprawdę robiłem wiele zadań dwoma sposobami − kombinatoryką i drzewkami − kombinatoryką jest dużo szybciej, drzewka to metoda "dookoła świata", niestety jak większość tego typu metod uwielbiana przez obecnych nauczycieli. Zrób sobie np. zadanie z losowaniem 3 kart z talii 52 kart drzewkiem i kombinacjami − zobaczysz różnicę. Ja robiłem to dwoma sposobami − kombinacjami zajęło mi może ze 3 minuty i 3 linijki w zeszycie, drzewkiem chyba z 10 minut i pół strony pisania. A dla nie mających wprawy uczniów trzeba wziąć poprawkę x 3 albo więcej. Myślę, że Tobie w szkole wpojono tę metodę jako "jedynie słuszną", a kombinatorykę jedynie liźnięto po łebkach albo wcale jej nie przerobiono, dlatego nauczyłaś się drzewkami. U mnie w szkole na początku pokazano kombinatorykę jako podstawę do rachunku prawdopodobieństwa, a drzewka były tylko w doświadczeniach dwu− i więcej etapowych, czyli w zadaniach typu: najpierw losujemy urnę wg określonej zasady, a potem kule z wylosowanej wczesniej urny − w tego typu zadaniach drzewka są idealną metodą, ale nie są najprostszą metodą w zadaniach z losowaniem kart czy kul z urny.

Marie: Wersja z drzewkiem jak dla mnie jest lepsza Dziekuje, dzieki rysunkom, a nie tylko suchym obliczeniom, latwiej mi pojac zadanie ß

KJK: Tylko problem jest taki że rozwiązanie P(B) robione "drzewkiem" jest błędne... Wystarczy porównać wynik P(B) "Nikka" oraz wynik "Gustlik" to są 2 różne wyniki. Jeśli już chcemy wykonać to drzewkiem to wynik musimy jeszcze podzielić przez 2, ponieważ to czy wylosujemy "pierw białą a potem czarną" czy "pierw czarną potem białą" to jeden i to samo ponieważ interesuje nas tylko fakt "różne kule". Kolejność nie ma tu znaczenia, gdy losujemy jednocześnie.

Bleee: KJK bzdury opowiadasz. To czy kolejność jest istotna czy też nie jest tutaj akurat kwestia pomijalna (czyt. KOLEJNOŚĆ NIE WPŁYWA NA WARTOŚĆ Prawdopodobieństwa w tym przypadku). Z tego też powodu zawsze doradzalem, aby robić uwzględniając kolejność. Pozatym gdzie Ty tutaj 2 różne wyniki?