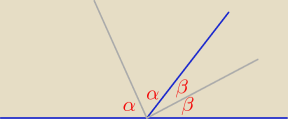
zad Kaasia: zadanie: Kąty \alpha i \beta są kątami przyległymi Kąt wyznaczony przez dwusieczne kątów \alpha i \beta ma miarę : rozwiązanie: Z określenia kątów przyległych mamy \alpha+\beta=180^o. Kąt (wypukły) utworzony przez dwusieczne kątów \alpha, \beta jest sumą \frac{1}{2}\alpha+\frac{1}{2}\beta, więc wobec powyższego jest on kątem prostym. nie rozumiem tego rozwiązania, dlaczego akurat z tego wynika że jest prosty? może ktoś to jaśniej objaśnić?

Bogdan: 2α + 2β = 180^o / :2 ⇒ α + β = ....

paziówna: kąty przyległe to takie, że ich suma to 180^o. masz więc: α + β = 180^o szukasz kąta utworzonego przez dwusieczne kątów α i β, dlatego bierzesz połowy tych obu kątów:

	1		1
		α +		β:
	2		2

α		β		1
	+		=		(α + β)
2		2		2

za α+β z pierwszego równania podstawiasz 180^o:

1		1
	(α + β) =		*180o = 90o
2		2

stąd jest to kąt prosty jaśniej? starałam się jak mogłam

Kaasia: tak, dziękuję już rozumiem

kami: dobre rozwiązanie

kami: bok rombu = 17 a jego dłuższa przekątna = 30 oblicz pole rombu

azcs: