matura
matematyka: tangens kąta ostego α jest równy p . wykaz ze (cosαα)−4= p4 + 2p2 +1
4 kwi 21:21
Jack: dobrze przepisany przykład? Nie ma tam czasem (cos2α)−4=....
4 kwi 21:36
matura: no prawie dobrze przepisany bo ma byc (cosα)−4
4 kwi 21:40
Jack: ok
4 kwi 21:40
matura: wiec jak to zrobic? wiesz?
4 kwi 21:43
Jack: próbuję...
4 kwi 21:45
matura: ok czekam
4 kwi 21:46
Jack:
| | 1 | | sin2α | |
( |
| )4=( ( |
| )2+1)2
|
| | cosα | | cos2α | |
| | 1 | | sin2α | | sin2α | |
( |
| )4=( ( |
| )2+1) * (( |
| )2+1) / * cos2α*cos2α
|
| | cosα | | cos2α | | cos2α | |
1=(sin
2α+cos
2α)
2
1=1
4 kwi 21:52
Jack: bez tych kwadratów po prawej stronie...
| | sin2α | | sin2α | |
....= ( |
| +1) * ( |
| +1) |
| | cos2α | | cos2α | |
4 kwi 21:53
Jack: a nie.. moment − można się zakrecić
4 kwi 21:54
matura: dzieki
4 kwi 21:57
Jack:
| 1 | | sin2α | |
| 4=( |
| +1)2
|
| cosα | | cos2α | |
| 1 | | sin2α | | sin2α | |
| 4=( |
| +1) * ( |
| +1) / *cos2α * cos2α
|
| cosα | | cos2α | | cos2α | |
1= (sin
2α+cos
2α) (sin
2α+cos
2α)
1=1
(można mnożyć przez cos
2α bez obawy mnożenie przez zero, gdyż cosα=0 dla α=
π2+kπ, gdzie
k∊Z, lecz w tych punktach tgα nie istnieje. A z zadania wiemy, że tgα istnieje i jest równy p)
4 kwi 21:58
matura: a mozna tak? zeby sin2α + cos2α = 1 i potem cos2α(1+p2)=1
4 kwi 21:59
matura: no no
4 kwi 22:00
Jack: ten pomysł z cos
2α(1+p
2)=1 jest też ok
cos
−4=(p
2+1)
2
4 kwi 22:07
matura: 
4 kwi 22:16
matura: a jak to :
7.11
pięciokąt ABCDE jest wpisany w okrąg o promieniu r. w pięciokacie tym boki AB i CD sa
rownoległe . ponadto AB =CD= r oblicz miarę kata AED.
4 kwi 22:17
Jack:
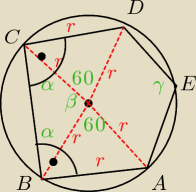
α=90
o−60
o=30
o
stąd β= 180
o−60
o=120
o
Stąd γ jest kątem wpisanym o opartym na kącie środkowym o mierze β+120
o, czyli γ=120
o.
4 kwi 22:30
Jack: przepraszam za sformułowanie "kąt wpisany opary na kącie środkowym"... jasne, że chodziło o
ten sam łuk...
4 kwi 22:34
matura: ok
4 kwi 22:39
Gustlik: Tangens kąta ostego α jest równy p . wykaz ze (cosαα)
−4= p
4 + 2p
2 +1.
Rysujemy trójkąt prostokątny. Zakładamy, że przyprostokątna przeciwległa a=p, przyprostokątna
| | p | |
przyległa b=1, wtedy tgα = |
| = p.
|
| | 1 | |
Z twierdzenia Pitagorasa obliczamy przeciwprostokątną c.
c
2 = a
2 + b
2
c
2 = p
2 + 1
2
c
2 = p
2 + 1 /
√
c
2 =
√p2 + 1
| | b | | 1 | |
cosα = |
| = |
| /4
|
| | c | | √p2 + 1 | |
| | 1 | |
(cosα)4 = |
| /−1
|
| | p4 + 2p2 + 1 | |
(cosα)
−4 = {p
4 + 2p
2 + 1}
cnd.
5 kwi 00:59