sda **kiełbasa***: 412. {logx+logy=1 {x²+y²=29 tym razem nie zależy mi na otrzymaniu rozwiązania, bo zrobiłam to zad. na dwa sposoby (algebraiczny− otrzymałam poprawny wynik i graficzny− nie zbyt dobrze) Proszę o wyjaśnienie czy ten przedstawiony poniżej jest zły czy po prostu niedokończony stąd zła odp? zał: x>0, y>0 (⇒będę rysować w I ćw. układu) {logxy=1 {(x+y)²−2xy=29 {xy=10 {(x+y)²=49 ⇒ x+y=7 v x+y=−7 y=−x+7 y=−x−7 teraz rysuję obie proste i zaznaczam dziedzinę. Dlaczego odpowiedzią nie jest fragment prostej y=−x+7 mieszczącej się w dziedzinie, a jedynie dwa punkty (2,5) i (5,2)? Gdy rozwiązuję to algebraicznie, otrzymuję oczywiście taki wynik... ale co złego jest w graficznym rozwiązaniu w razie potrzeby mogę spróbować załaczyć obrazek fragmentu układu współrzędnych z prostą i dziedziną

Jack: x,y>0 czyli nie na sensu rozpatrywać x+y=−7 bo któraś z liczb musiałaby być ujemna. Ponadto dobrze zapisałaś ze patrzysz tylko na pierwszą ćwiartkę (ale dla tego drugiego równania: x+y=7).

miki:

	10
Ja proponuję narysować gałąź hiperboli y=		w I ćw.
	x

i ćwiartkę okręgu S(0,0) i przez punkty okręgu A x= 5 to: 25 +y²= 29 => y² = 4 => y = 2 ( bo y>0) A( 5,2) r= ISAI i wszystko ładnie wyjdzie

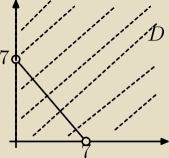
kiełbas: zamieszczam sporządzony przeze mnie obrazek. Proszę o wyjaśnienie dlaczego odpowiedzią nie jest cały ten fragment prostej? tylko dwa punkty

kiełbas: miki, zrozumiałam gdzie popełniam błąd. dziękuję bardzo Tobie i Jackowi. pozdrawiam