trojkaty Sarcia: Pomocy W trojkat rownoramienny o kacie przy podstawie 30 stopni wpisano okrag o promieniu 2. Oblicz pole tego trojkata.

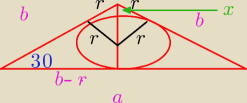Donia : rysunek nie jest za piekny ale powinien pomoc x+r = 2√2 x=2√2 +2

	2r+x
sin30 =
	b−r

b=5+2x b=2√2 +3 a juz latwo obliczyc a z tego pole

Sarcia: Nie rozumiem zbytnio Dlaczego, te odcinki przy wierzcholku tez sa rowne r

	1
i nie wiem tez dlaczego		a = b−r
	2

Prosze o wytlumaczenie

Sarcia: Moglby mi ktos to bardziej wytlumaczyc Prosze....

Sarcia: Prosze Was o POMOC! Z gory dziekuje wybawcy

Donia : Zle to zrobiłam. Chyba też nie umiem tego zadania.

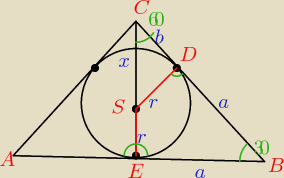uliko: W trójkącie SDC, kąt C ma 60st bo 180−30−90=60 tak więc:

	r
sin60=
	x

√3		2
	=
2		x

	4√3
x=
	3

	2√3
Znając x oraz r z Tw.Pitagorasa obliczamy b, b=
	3

Z trójkąta CEB mamy:

	x+r
tg30 =
	a

.... a=4 Znamy już wszystkie dane potrzebne do obliczenia pola i obwodu.

Anna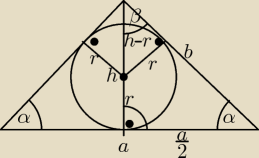: Dane: r=2, α= 30⁰ P_Δ = ?

	h
		= tgα
	a   2

	h		√3
		=
	a   2		3

	a√3
3h =		/:3
	2

	a√3
h =
	6

	r
		= sinβ
	h−r

	2
		= sin600
	h−2

	2		√3
		=
	h−2		2

(h−2)√3 = 4 h√3 − 2√3 = 4 h√3 = 4 + 2√3

	4+2√3		2√3(2+√3)
h =		=
	√3		3

	a√3		2√3(2+√3)
Zatem:		=		/*6
	6		3

a√3 = 4√3(2+√3) a = 4(2+√3)

	1		1		2√3(2+√3)		4√3
PΔ −		ah =		* 4(2+√3)*		=		(2+√3)2 =
	2		2		3		3

	4√3		4√3
=		(4+4√3+3) =		(7+4√3)
	3		3

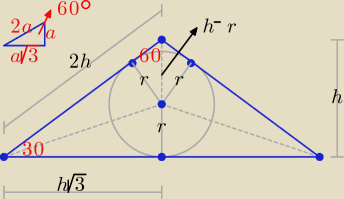Bogdan: Dzień dobry.

r		2		√3		4
	= sin60o ⇒		=		⇒ h =		+ 2
h − r		h − 2		2		√3

	1
Pole trójkąta P =		* 2h√3 * h
	2