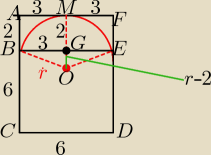
styczne i sieczne Hashiri: Witam. Bok kwadratu BCDE ma dlugosc 6 (rysunek), a przekatna prostokata ACDF ma dlugosc 10. Oblicz promień okregu, ktorego lukiem jest BE(czerwony luk). bardzo prosze o jak najszybsza pomoc

Hashiri: Bardzo prosze o pomoc Plisssss

Zaks: Strasznie trudne to zadanie , nei moge zrobic Tez bym prosil o pomoc

Jack: połowa |BE|? (zależy czy dobrze czytam ten rys.)

Hashiri: Ten luk czerwony jest oparty na odcinku |BE| i styczny do |AF|

Godzio: ale to w takim razie to tak jak mówi Jack promien to polowa boku BE

Jack: tylko po co ta informacja o przekątnej Dezorientująca nieco...

Hashiri: Nierozumiem to nie jest rowno polowa okregu w odpowiedziach do tygo zadania jest 3.25, czyli blisko 3. Dlatego jest podana ta przekatna. To jest zadanie z podrecznika z dokladnie takim samym rysunkiem. Czerwony luk jest styczny do |AF| i oparty na |BE| oraz to NIE jest polowa calego okregu. Wlasnie to zalezy od tego jaka jest ta szerokosc prostokata, pewnie po to jest ta przekatna.

Hashiri: To wie moze ktos jak to zadanko rozwiazac

Nikka: Nie mam pewności, ale tak sobie myślę, że środek okręgu będzie leżał na symetralnej odcinka |BE|. Narysowałabym obie przekątne prostokąta oraz styczne do okręgu w punktach B i E. Następnie dwie proste prostopadłe do stycznych przechodzące przez punkty B i E (punkty styczności). Punkt przecięcia tych prostych będzie środkiem okręgu. I zastanawiam się czy środek okręgu nie pokryje się z punktem przecięcia przekątnych prostokąta...

Jack: wiesz co, zrobiłem sobie kilka rysunków i faktycznie tak wychodzi, że to może być punkt przecięcia przekątnych... choć może być ciężko to udowodnić

miki: Ok pomogę IADI=10 ICDI= 6 to: IACI= √10²− 6²= 8 zatem : IABI= 8−6= 2 więc IMGI= 2 to IOGI= r−2 i IOBI= r z ΔBGO mamy: r²= (r−2)²+3² r² = r² −4r +4+9 4r= 13 r= 3¹₄ = 3,25

Jack: hehe

Nikka: no właśnie − może tak być, ale nie musi... próbowałam jeszcze inaczej... nie wiem tylko czy możemy założyć, że ten okrąg będzie wpisany w prostokąt (czworokąt) i wtedy

	2P
r =		P − pole, Obw − obwód
	Obw

niestety niezupełnie zgadza mi się wynik − wyszło mi 3, 43

Eta:

Jack: to było prostsze niż myśleliśmy brawo za przytomność umysłu

Nikka:

Eta:

Eta: Pozdrawiam Was świątecznie

Hashiri: Wielkie dzieki, naprawde mi to pomoglo. Gratuluje

Jack: Pozdrawiamy

miki:

Nikka: Dzięki Eto i wzajemnie

Hashiri: Mam jeszcze np takie zadanko: Czy istnieje liczba dwucyfrowa o tej wlasnosci, ze po przedstawieniu cyfry jednosci na pierwsze miejsce otrzymamy liczbe dwa razy wieksza od danej liczby Moje rozumowanie jest takie, tylko nie wiem czy dobre: l. dwucyfrowa to 10a+b 10b+a=2(10a+b)=20a+2b 8b=19a, wiedzac ze a,b∊≤0,9≥\a=0 to a=8, a b=19 czyli NIE ISTNIEJE Dobrze to rozumiem

Jack: poszukujesz NWW (8, 19)... 19 jest liczbą pierwszą więc dopiero 19*8 jest NWW(19,8), stąd a=8, b=19 a to jest sprzeczne bo a,b≤9.

miki: ok

Hashiri: Dzieki, a jak to zrobic zadanie : Czy liczba a=5042176803021 jest szescianem liczby naturalnej Pewnie trzeba wiedziec wlasnosci szescianow liczb naturalnych.

Jack: http://www.matematyka.pl/19739.htm

Hashiri: Czesto sie przydaje robic szybko takie przeksztalcenie:

10ka		10
	=10+
ka−1		ka−1

Tylko ja tego nie widze Moglby ktos to rozwinac

Jack:

10ka		10(ka−1)+10		10(ka−1)+10		10
	=		=		=10+
ka−1		ka−1		ka−1		ka−1

Jack: wiesz skąd się wziął drugi krok?