sd ***kiełbasa***:

	Ilog(x+1)I
rozwiązać nierówność: 410.		≤log(x+1)2 odp:
	x2−1

	√2		√6
x∊(−1,−		>U<0,1)U<		,∞)
	2		2

Tomek.Noah: nie robilem takiego typu zadan a pokaze swoja mysl bo zawsze to cos uklad: lub uklad: x>−1 x>−1 log(x+1)≥0 log(x+1)<0

log(x+1)		−log(x+1)
	≤2log(x−1)		≤−2log(x−1)
x2−1		x2−1

Tomek.Noah: ale czegos brakuje i nie wiem wlasnie czego

kiełbasa: może napiszę jak ja robiłam i mi pomożesz? zał: {x+1>0 x>−1 {x²−1≠0 x≠−1 i x≠1 {(x+1)²>0 x≠−1 D=(−1,∞)−{1} 1. log(x+1)≥0⇔x≥0 lub 2. x<0

log(x+1)
	≤2log(x−1)
x2−1

i tu się zaczęły schody, bo nie wiem jak to przekształcać próbowałam tak: log(x+1)≤2*(x²−1)*log(x−1) log(x+1)≤log(x−1)^2x2−2 (x+1)≤(x−1)^2x2−2 i nie wiem czy był sens doprowadzić do takiej postaci, bo nie wiem co dalej. Drugi przypadek analogicznie

Tomek.Noah: ale sry twam w logarytamh po obu stronah jest log(x+1) wiec chyba byl sens

Tomek.Noah: bo ostatecznie masz (x+1)≤(x+1)^2x2−2 a to jest jak wiesz ja nie wiem bo tego nie bralem 1≤2x²−2

Tomek.Noah: uuwzglednijajac dziedzine moze cos z tego bedzie

Jack: czemu zmieniacie znak w argumencie logarytmu po prawej stronie na "minus" po rozpisaniu modułu? To celowy zabieg czy omyłka?

Jack: Dokładnie tak! Spróbujmy tą drogą.

Jack: 1) x≥0

log (x+1)
	≤ 2log (x+1) / * (x2−1)
x2−1

1a) gdy x∊(−1,1) log (x+1)≥ 2*(x²−1)*log (x+1) x+1≥ (x+1)^2x2−2 1≤ 2x²−2 ³₂≤x² x∊(−∞, ^√6₂>∪ <^√6₂, +∞) Biorąc warunki mamy: x∊[(−∞, −^√6₂>∪ <^√6₂, +∞)] ∩ (−1,1) ∧ x≥0 ⇒ x∊∅ 1b) x∊(−∞,−1)∪ (1,+∞) log (x+1)≤ 2*(x²−1)*log (x+1) x+1≤ (x+1)^2x2−2 1.b.1 x∊(−∞,−1) 1≥2x²−2 ³₂≥x² x∊ {(−^√6₂, ^√6₂) ∩ [(−∞,−1)∪ (1,+∞)]} ∧ x∊(−∞,−1) ∧ x≥0 ⇒ x∊ ∅ 1.b.2 x∊(1,+∞) 12x²−2 ³₂≤x² x∊ {[(−∞,^√6₂> ∪ <^√6₂,+∞) ∩ [(−∞,−1)∪ (1,+∞)} ∧ x∊(1,+∞) ∧ x≥0 ⇒ x∊ <^√6₂,+∞) 2) x<0

−log (x+1)
	≤ 2log (x+1) / * (x2−1)
x2−1

2a) gdy x∊(−1,1) −log (x+1)≥ 2*(x²−1)*log (x+1) (x+1)⁻¹≥(x+1)^2x2−2 −1≤2x²−2 1≤2x² x²≥¹₂ Zatem x∊ [(−∞, −^√2₂>∪ <^√2₂>, +∞)] ∩ (−1,1) ∧ x<0 ⇒ x∊ (−1, ^√2₂> 2b) gdy x∊(−∞,−1)∪(1,∞) wyjdzie znowu x∊∅. Nie chce mi wyjść (na początku) fragment x∊<0,1)

Jack: w 2a) x∊(−1,−^√2₂>

Tomek.Noah: wg mnie juz napoczatku jest zle nie dawaj zalozen i nie posbywaj sie tak mianownika przenies lewa strone na prawa a potem zastosuj przeksztalcenie wilomianowe to ejst moja ocena ja tego jeszcze nie przerabialem wie cwies..

Jack: 1a) gdy x∊(−1,1) rozpatrzmy przypadek gdy x∊<0,1) [ 1a.1] oraz x∊(−1,0) [ 1a.2] 1a.1 x∊<0,1) wówczas: x+1≥(x+1)^2x2−2 1≥ 2x²−2 (ponieważ podstawa wykładnika jest >1) ³₂≥x² x∊(−^√6₂,^√6₂) ∧ x∊<0,1) ∧ x≥0 ⇒ x∊<0,1) 1a.2 x∊<−1,0) x∊∅ ponieważ musi być spełniony również warunek: x≥0 Wychodzi wiec suma podanych w odpowiedziach przedziałów. Uff

Jack: pozbywając się mianownika muszę coś założyć na temat wyrazu, przez który mnożę. Można tak robić, pamiętając, że jak się mnoży przez ujemną liczbę, to zmienia się znak.

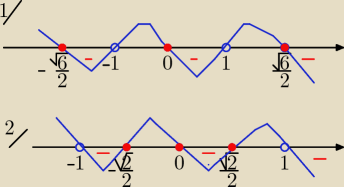
miki: założenia: x +1>0 i x ≠ − 1 i x ≠ 1 => x€( −1, 1) U ( 1, ∞) 1/ dla log (x+1) ≥0 ,czyli dla x+1 > 1 => x >0 mamy po zamianie na iloczyn: [ log(x+1)−(x²−1)*2log(x+1)]*(x²−1) ≤0 [log(x+1) ] (1−2x²+2)*(x−1)(x+1) ≤0 [log(x+1)] *(3−2x²)(x−1)(x+1)≤0 miejsca zerowe: x =0 v x= −√6/2 v x= √6/2 v x= 1 v x= −1 rysunek 1) "fala' uwzględniając ,że x >0 i x€ < −√6/2 , −1) U <0,1) U < √6/2, ∞) 1) odp: x€ <0,1) U < √6/2, ∞) podobnie dla : 2) log (x+1) <0 , czyli dla x <0 mamy: [−log( x+1) −(x²−1)*2log(x+1)]*(x²−1) ≤0 [log(x+1)]*( −1 −2x²+2)(x+1)(x−1) ≤0 [log(x+1)]( 1−2x²)(x+1)(x−1) ≤0 miejsca zerowe: x= 0 v x = −√2/2 v x = √2/2 v x= −1 v x= 1 rysunek 2) "fala} uwzględniając x <0 otrzymamy ; x€(−1, −√2/2> rozwiazaniem pierwotnej nierówności jest suma przedziałów z 1) , 2)

	√2		√6
Odp: x€(−1, −		> U <0,1) U <		, ∞)
	2		2

***kiełbasa***: miki, dziękuję, dobrze, że jesteś. pomożesz mi jeszcze w tym: 411.x ^{1₄(7+log₂x)}≥2^1+log₂x

	1
odp: x∊(0,		>U<1,∞)
	16

miki: W/g moich obliczeń , to odp. jest:

	1
x€( 0,		> U <2, ∞)
	16

sprawdź , czy dobrze podałaś tę odp

kiełbasa: masz rację. 2, mógł(a)byś podać rozwiązanie?

Aneta: KIEŁBASA CZY UMIAŁBYS ROZWIĄZAĆ MOJE ZDANIE? Odcinek PQ o długośc 13 cm zrutowano prostopadle na płaszczyznę π. Oblicz długość rzutu tego odcinka, wiedząc, że punkty P i Q leżą po tej samej stronie płaszczyzny π w odległościach odpowiednio równych 8 cm i 3 cm.

kiełbas: jestem kobietą nick to nazwisko autora zbioru, z którego dodaję zadania. nie robiłam tego typu zadań, więc wolałabym się dowiedzieć czy masz odpowiedź, bo nie jestem pewna, czy policzyłam to o co pytają.

miki: ok założenie x >0 logarytmujesz logarytmem o podstawie 2 obydwie strony otrzymasz: ¹₄(7+log₂x)*log₂x ≥ (1+log₂x)*log₂2 podstawiasz za log₂x= t otrzymasz: ¹₄t²+⁷₄t −1 −t≥0 /*4 t²+3t −4 ≥0 Δ= 25 t₁= 1 v t₂= −4 to ( log₂x−1)(log₂x+4) ≥0 miejsca zerowe: x= 2 v x= ¹₁₆ uwzględniasz założenie: x >0 odp: x€ ( 0, ¹₁₆> U < 2,∞)

miki: I co? ... pasuje?