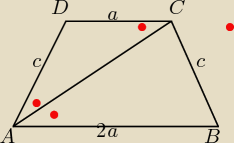
 W trapezie równoramiennym ABCD w ktorym AB||CD oraz AB= 2a i CD=a przekątna AC azawiera sie w
dwusiecznej kata DAB oblicz dlugosc promienia okregu wpisanego w trojkat ABC
Czerwony ta Kat L katy na przemianlegle czyli Trojkat ACD jest rownoramienny czyli
c=a
ale dalej nie wiem co bo gdy chce z twierdzenia sinusow obliczyc L wychodzi glupie rownanie
znaczy glupie da sie je rozwiazac no ale zajmie 3/4 stroni i moim zdaniem musi byc jakis inny
sposob
rownie
asinL=2asin(180−3L)
Musi byc inny sposob
W trapezie równoramiennym ABCD w ktorym AB||CD oraz AB= 2a i CD=a przekątna AC azawiera sie w
dwusiecznej kata DAB oblicz dlugosc promienia okregu wpisanego w trojkat ABC
Czerwony ta Kat L katy na przemianlegle czyli Trojkat ACD jest rownoramienny czyli
c=a
ale dalej nie wiem co bo gdy chce z twierdzenia sinusow obliczyc L wychodzi glupie rownanie
znaczy glupie da sie je rozwiazac no ale zajmie 3/4 stroni i moim zdaniem musi byc jakis inny
sposob
rownie
asinL=2asin(180−3L)
Musi byc inny sposob

 Dzieki za pomoc
Dzieki za pomoc 
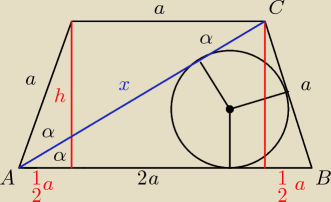
| 1 | ||
h2 = a2 − | a2 | |
| 4 |
| 3 | ||
h2 = | a2 | |
| 4 |
| √3a | ||
h = | ||
| 2 |
| 2a * h | √3a | a2√3 | ||||
P = | = a * | = | ||||
| 2 | 2 | 2 |
| 9 | 3a2 | 12a2 | ||||
x2 = | a2 + | = | = 3a2 | |||
| 4 | 4 | 4 |
| 2P | a√3 | a√3(3−√3) | a(3√3 − 3 | |||||
R = | = | = | = | = | ||||
| 2a + a + a√3 | 3 + √3 | 6 | 6 |
| a(√3−1) | ||
| 2 |
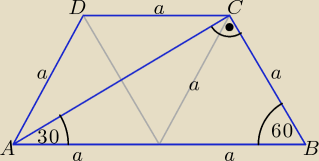 Można dość łatwo ustalić miary pokazane na rysunku. Ponadto: |AC| = a√3.
Można dość łatwo ustalić miary pokazane na rysunku. Ponadto: |AC| = a√3.
| 1 | ||
Długość promienia r okręgu wpisanego w trójkąt ABC: r = | (|AC| + |BC| − |AB|), | |
| 2 |
| 1 | 1 | |||
czyli r = | (a√3 + a − 2a) = | a(√3 − 1) | ||
| 2 | 2 |
