zad matthew: Cześć mam zadanie z parametrów: a) dla jakich wartości parametru m nierówność (x−3m)(x−m−3)<0 jest spełniona przez każdą liczbę rzeczywistą należącą do przedziału <1,3> b) pierwiastki x₁, x₂ równania 2x² −2(2m+1)x+m(m−1) = 0 spełniają warunek x₁<m<x₂ ? proszę o jakąś podpowiedz...

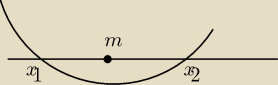
Godzio: b) 2x² − 2(2m+1)x + m(m−1) = 0 f(m) < 0 2m² − 2(2m+1)m + m(m−1) < 0 dokończ to i to będzie odp

Godzio: Ja bym to tak zrobił ale głowy nie dam (x−3m)(x−(m+3) ) < 0 (x−1)(x−3) < 0 x∊(1,3) 1 = 3m m + 3 = 3

	1
m =		m = 0
	3

	1
m∊(0,		)
	3

Jack: b) może można też wymnożyć nawias, znaleźć Δ>0 i x₁=1, x₂=3 (lub Δ>0 , x₁=3 x₂=1).