Rozwiąż nierówność. Logarytmy i funkcja wykładnicza. Keisim: Kolejne pytanie. Jak ugryźć taką nierówność:

log x − 1
	≥ 0
(3 − 3x)(x − 4)

	x
Zacząłem od licznika, przekształciłem go w → log
	10

Próbowałem też → 0 = log 1... Trzeba sprawdzić czy mianownik ≥ 0, żebyśmy mogli go pominąć? Nie mam pomysłu, proszę pomóżcie...

Jack: a) licznik jest >0 dla x∊(10,∞) b) (3−3^x)>0 dla x∊(−∞,1) c) (x−4)>0 dla x∊(4,∞) Pozbieraj możliwości...

Godzio: x czy x − 1 jest w logarytmie

Keisim: Jack ma rację. Godzio, log x, w przeciwnym razie złapałbym to w nawias.

Keisim: Chociaż właściwie... czy tak powinno być rozwiązane zadanie?

Keisim: Rozumowanie Jacka jest chyba w porządku, ale jak je zastosować do nierówności? Jeżeli wszystkie są dodatnie to nierówność ≥0, ale przecież jest to tylko jedna możliwość... kolejna to gdy licznik ≤0 i jeden z nawiasów w mianowniku też ≤0 albo licznik ≥0 i obydwa nawiasy w mianowniku ≤0... Czy Jack to uwzględnił a ja po prostu nie rozumiem czegoś?

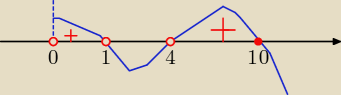
miki: założenie: x >0 , x≠ 4 x≠1 Zamieniamy na postać iloczynową ( logx −1)(3−3^x) ( x −4)≥0 miejsca zerowe x= 10 x= 1 x= 4 wykres ( "fala") od prawej strony od dołu odp: x€ ( 0, 1) U (4, 10>

Keisim: Dzięki bardzo Miki, to mi bardziej rozjaśniło.