stereometria !!!!rybcia!!!!!!!!!!!: Dany jest prostopadłościan o podstawie kwadratowej i wysokości h. 1. Wyznacz pole przekroju prostopadłościanu płaszczyzną przechodzącą przez przekątne sąsiednich ścian bocznych wychodzące z jednego wierzchołka, jeśli wiadomo, że kąt między nimi ma miarę alfa. 2. Wyznacz alfa, tak aby pole przekroju prostopadłościanu płaszczyzną przechodzącą przez przekątne sąsiednich ścian bocznych wychodzące z jednego wierzchołka było równe P= ^h2₂

Godzio:

	h2sinα
Czy wynik to może		?
	2*√cosα

!!!!rybcia!!!!!!!!!!!: nie wiem jaki jest wynik niestety...

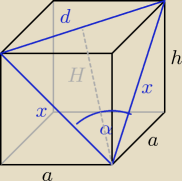Godzio: Mam nadzieję że dobrze a² + h² = x² d² = x² + x² − 2cosα * x² 2a² = 2a² + 2h² − 2cosα * (a² + h²) 0 = 2h² − 2cosα * a² − 2cosα *h² 2cosαa² = 2h² − 2cosα *h²

	h2 − cosα *h2
a = √
	cosα

	1
H2 = a2 + h2 −		*2a2
	4

H² = h² + 0,5a²

	h2 − cosα *h2
H2 = h2 +
	2cosα

	h2 − cosα *h2		h2cosα + h2
H = √ h2 +		= √
	2cosα		2cosα

	Hd		h2cosα + h2		h2 − cosα *h2		1
P =		= √		* √		*√2 *		=
	2		2cosα		cosα		2

	h2cosα + h2		h2 − cosα *h2		1
√		* √		*		=
	cosα		cosα		2

h2		(1+cosα)(1−cosα)		h2		1 − cos2α
	* √		=		* √
2		cosα		2		cosα

h2		sin2α		h2sinα
	* √		= =
2		cosα		2*√cosα

Godzio: robiąc podp. b stwierdziłem że gdzieś jest błąd także będe szukac

Godzio:

	Hd		h2cosα + h2		a√2
P =		= √		*		=
	2		2cosα		2

	h2(cosα + 1)		h2(1−cosα)		√2
√		* √		*		=
	2cosα		cosα		2

h		√2		cosα + 1		1−cosα
	* h *		* √		* √		=
√2		2		cosα		cosα

h2		1−cos2α		h2		sin2α		h2
	* √		=		* √		=		* tgα
2		cos2α		2		cos2α		2

Teraz powinno być dobrze