losowanie kul z urny betsy: W urnie jest 5 kul białych, 2 czerwone, 3 czarne. Losujemy kolejno 2 kule. jakie jest prawdopodobieństwo wylosowania 2 kul tego samego koloru, wiedząc że wylosowana kula nie wraca do urny przed wylosowaniem drugiej kuli? ma wyjsc 28/90

Nikka: łatwo będzie z drzewka

betsy: hmm nigdy nie robiłam z drzewka, w szkole nauczycielka pominela ten sposob... teraz powtarzam do matury, ale chyba mam zaleglosc z tego

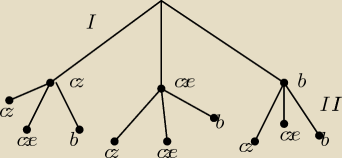
Nikka: cz − czarna cze − czerwona b − biała W pierwszym losowaniu (na odpowiednich gałęziach drzewka) będziemy mieli:

	2
cz −
	10

	3
cze −
	10

	5
b −
	10

W drugim (interesują nas tylko kule tego samego koloru):

	1
cz − cz −
	9

	2
cze−cze −
	9

	4
b−b −
	9

	2		1		3		2		5		4		28
P(A) =		*		+		*		+		*		=
	10		9		10		9		10		9		90

Nikka: te ułamki na ramionach drzewka to prawdopodobieństwa wylosowania kuli czerwonej , czarnej , białej ...

Nikka: ni ejestem ekspertem, ale mam nadzieję , ze jest ok

betsy: umie to ktoś rozwiązać w inny sposób?

Nikka: zdaje się można z kombinacji... |Ω| = C²₁₀ = 45 |A| = C²₅ + C²₂ + C²₃ = 10 + 1 + 3 = 14

	14
P(A) =
	45

28		14
	=
90		45