zad matthew: Cześć, mam takiezdanie z parametrem: 1) dla jakich wartości parametru m suma kwadratów pierwiastków równania jesr równa S x² + 5x + 20m − 8 = 0 S = 400 i jeszcze takie: 2) Dla jakich wartości parametrówm: suma odwrotności pierwiastków równania x² + mx − 16 = 0 jest równa −4? 1) czy w tym zadaniu należy zacząć od: x²₁ + x²₂ = S ? cały czas wychodzi mi zły wynik

	1		1		−b
2) a tutaj tak:		+		= −4 ⇒		= −4 ?
	x1		x2		c

proszę o pomoc...

Godzio: pomoge

Godzio: sprawdź treść moge się założyć że powinno być x² + 5mx + 20m − 8 = 0

matthew: masz racje

Godzio: Zaczne od Δ ≥ 0 Δ = 25m² − 80m + 32 ≥ 0 25m² − 80m + 32 ≥ 0 Δ = 3200 √Δ = 40√2

	80−40√2		8−4√2
m1 =		=
	50		5

	8+4√2
m2 =
	5

	8−4√2		8+4√2
m∊ (−∞		> ∪ <		,∞)
	5		5

I teraz tak jak mówiłeś x₁² + x₂² = (x₁+x₂)² − 2x₁x₂ = 25m² − 40m + 16 = 400 25m² − 40m + 16 = 400 25m² − 40m − 384 = 0 Δ = 40000 √Δ = 200

	40−200		−160		1
m1 =		=		= −3
	50		50		5

	40 + 200		240		4
m2 =		=		= 4		oba pierwiastki należą do założenia
	50		50		5

Godzio: 2) x² + mx − 16 = 0 Δ = m² + 64 ≥ 0 m∊R

1		1		−b
	+		=		Czyli tak jak pisałeś i teraz podstawiasz wartości i wyliczasz
x1		x2		c

−m
	= − 4
−16

−m = 64 m = − 64

matthew: dzieki zapomnialem o tym przeksztalceniu x²₁+ x²₂ = (x₁+x₂)² − 2x₁x₂ dlaczego Δ ≥ 0 ?

Godzio: bo nie jest w treści powiedziane że dwa różne pierwiastki

matthew: mam pytanie.... co to znaczy odwrotność sumy pierwistków jakiegoś równiania jest dodatnia odwrotność sumy pierwistków − wiem jak wygląda, związane z nim były poprzednie zadania, ale dodatnia? o co chodzi?

	−b
czy to ma wyglądać tak:		> 0 ? czy muszę rozwiązać jeszcze x1, x2
	c

matthew: x₁*x₂ > 0 ?

Godzio: no właśnie nie tak odwrotność jest głównym działaniem

	1
w takim tazie:		> 0 jest dodatnia
	x1+x2

Godzio: inaczej:

a
	> 0
−b

matthew: no nareszcie... w koncu mi wyszło dzieki

matthew: mam jeszcze coś takiego.... dla jakich wartości parametru m: równanie x² + mx − 2 = 0 ma dwa pierwiastki, z których jeden jest sinusem, a drugi cosinusem tego samego kąta? mam tak m ∊(−∞, 4 − 2√2) ∪ ( 4 + 2√2 , + ∞) i dalej nie wiem.... proszę o pomoc

Godzio: to masz dane w poleceniu to m ? bo z delty to tak nie wyjdzie

Godzio: Tutaj trzeba użyć wzoru na jedynkę trygonometryczną sin²α + cos²α = 1 x₁² + x₂² = 1 (x₁+x₂)² − 2x₁x₂ = 1 a dalej myślę że sobie juz poradzisz

matthew: no jak to .... napisze

matthew: Δ>0 Δ = m² − 8m + 8 Δ = 64 − 4 * 8 = 64 − 32 = 32 √Δ = 4√2

	8 − 4√2
m1 =		= 4 − 2√2
	2

m₂ = 4+2√2 ramiona skierowane do gory, bez m. zerowch, wychidzi mi: (−∞, 4 − 2√2) ∪ ( 4 + 2√2 , + ∞)

Godzio: Δ = m² − 4 * 1 * (−2) = m² + 8 > 0 m² > − 8 m∊R

matthew: Godzio a jak bym mial polecenie: "jeden pierwiastek jest równy sinusowi, a drugi cosinusowi tego samego kąta ostrego", zmienia to coś w stosunku do podpunktu poprzedniego?

Godzio: tylko że znowu z twojego rozwiązania wynika : x² + mx + 2m − 2 , a ty napisales x² + mx − 2 jeśli ma być ten pierwszy przypadek to sie zgadza wszystko w Twoim rozwiązaniu

matthew: wiesz co, ja sie tam pomyliłem, delta mi jednak dobra wyszła, a wzór powinien być taki: x² + mx − 2m − 2 = 0 sorki za wprowadzanie w bład.....

matthew: no wlasnie

Godzio: nie

matthew: yyy tzn + 2m

Godzio: to "nie" tyczy się tego zadania "jeden pierwiastek jest rowny sin. ..."

matthew: ok

matthew: mam jeszcze takie zadanie: Dla jakich wartości parametru m: każdy z dwóch różnych pierwiastków równania x² − 6mx + 2 −2m + 9m² = 0 jest wiekszy od 3 Δ ≥ 0 wyszło mi z delty, ze: m∊<1 + ∞) i nie wiem co dalej... prosze o pomoc

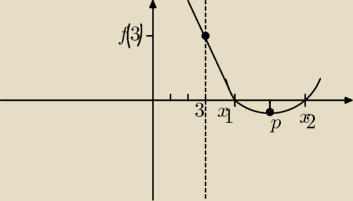
Godzio: "każdy z dwóch różnych pierwiastków" => Δ > 0 mając dane z rysunku tworzymy układ równań: {Δ > 0 {p > 3 {f(3) > 0 rozwiąż go i znajdź część wspólną wszystkich rozwiązań

zajączek:

Godzio: Przypomniałem sobie jak to mi podobne zadanie tłumaczono

zajączek: Miło mi ,że .... " nauka nie poszła w las"

Godzio:

matthew: Godzio jak mam zapisać wzór dla p > 0?

matthew: a juz chyba wiem

matthew: udało sie {8m − 8 > 0 {3m>0 {9m² − 20m + 11>0

	1
m∊(1		, + ∞)
	9

matthew: Godzio, a z jakich ksiązek korzystałeś? pamietasz może? bo ja mam tylko pazdry... z checia bym cos kupil jeszcze

matthew: mam podobne zadanie tylko, że pierwiastki mają być mniejsze od 4 zrobiłem tak: {m² − 16>0

	−m
{		>0
	2

{4m + 20 >0 mam taką odpowiedz: m∊(−5, −4),...... natomiast rozwiazanie w książce jest takie: m∊(−5, −4)∪(4, +∞) prosze o sprawdzenie...

matthew: wzór jest taki: x² + mx + 4 = 0

zajączek: Napisz jakie jest to równanie, bo nie wiem ......a to ważne ! jeżeli a >0 to: 1) Δ>0 2) x_w < 4 3) f(4) >0 rozwiąż układ tych warunków jeżeli a<0 to: 1)Δ>0 2) x_w<4 3) f(4) <0

matthew: ahaaaa ok juz wszystko wiem.... tzn co do tego zadania

zajączek: zatem ten pierwszy układ warunków , bo a>0 −−− ramiona paraboli do góry taką odp; otrzymasz m€ ( −5, −4) U ( 4, ∞)

matthew: moment.... już wiem jak zmieniają sie znaki, gdy współczynnik jest dodatni bądź ujemny dla pierwiastków mniejszych od danej liczby natomiast jeśli pierwiastki są większe od liczby, a współczynnik jest ujemny to jak wtedy wygląda układ? Dla wspołczynnika dodatniego: Δ>0, x_w >0, f(x) > 0 ? tak jak na górze...

Godzio: No już wróciłem No więc ja się przymierzam do kupna jakiś zbiorów jeszcze ale póki co to: http://www.aksjomat.torun.pl/index.php?products=product&prod_id=90 + to co w szkole, ale sobie jeszcze dokupię rozszerzenie do tego Aksjomatu + jeszcze poszukam jakiś ciekawych ale to za jakies 2 tygodnie

zajączek: liczba t , i a<0 −−− ramiona do dołu to wierzchołek musi być na na prawo od zadanej liczby "t" i f(t) >0 czyli mamy układ: Δ>0 x_w > t f(t) >0

matthew: wiesz co ja tez mam tą ksiązkę, wydawnictwa aksjomat poziom rozszerzony. Okładkę ma czerwoną. Racja z niej też korzystam ale jest dosyć cięzko

matthew: tzn. ze i dla a<0 i dla a >0 układ wygląda tak samo? chodzi mi o znaki...

Godzio: Musze się jeszcze nauczyciela dopytać jaki sobie zbiór kupić do rozszerzenia. A może zajączek coś doradzi ?

matthew: ...ech znowu mi xle wychodzi... Δ>0 x_w<0 f(t) >0 {m²−16>0

	−m
{		< 0
	2

{4m+20>0 m²−16>0 (m−4)(m+4) = 0 m = 4 m = −4 m∊(−∞, −4)∪(4, +∞)

−m
	< 0/4
2

−2m<0 m>0 m∊(0, +∞) 4m+20>0 4m>−20 m>−5 m∊(−5,+∞) odp. m∊(4, +∞) prosze o sprawdzenie...

zajączek:

−m
	< 4
2

m > −8