zadanie rozszerzone Ola: Ktoś potrafi rozwiązać? Kąt dwuścienny między dwiema sąsiednimi ścianami bocznymi ostrosłupa prawidłowego czworokątnego ma miarę 120. Znajdź miarę kąta nachylenia ściany bocznej do płaszczyzny podstawy.

xyz: ponawiam

tom: 10 minut

Ola: i jak, będzie pomoc czy nie?

tom:

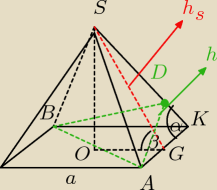
	a√2
a− bok podstawy β − szukany kąt; ∡ BDA = 120o ∡OAD =30o |OA|=
	2

|OA|		√3		√2		h		√2
	=cos30o=		→h=a		z ΔAKD sinα=		=
h		2		√3		a		√3

	|KG|		|OG|		1
z ΔKSG ctgα=		ale z ΔGSO cosβ=		cosα=√1−sin2α=
	hs		hs		√3

	1		√3		√2
cosβ = ctgα =		*		=		stąd β=45o
	√3		√2		2

emm: Dlaczego ∡ GKS to kąt alfa, skoro kąt alfa to kąt ∡ BDA?

a: prosze o wytlumaczenie.

Siti: autor rozwiązania kątem α nazwał kąt GKS, a kat BDA pozostawił po prostu kątem BDA.

Siti: Poza tym kąt BDA jest dany w treści i jego miara jest znana, więc nie trzeba go oznaczać α

emm: Ok dziekuje i przepraszam za nieogarniecie

pablo 3c: Bardzo mierne