 zad. 1
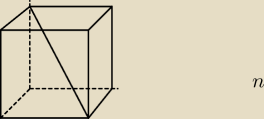
oblicz sinusa kata miedzy przekątną szescianu, a jego płaszczyzna podstawy.nic wiecej nie jest
podane. (rysunek)
zad. 2
ile scian i ile krawedzi ma ostrosłup o 20 wierzchołkach?
zad.3
Wszystkie krawedzie ostrosłupa prawidłowego czworokatnego maja jednakowa długość. Oblicz
objętosc ostrosłupa.
zad. 4
oblicz długosc przekatnej szescianu o krawedzi 12 cm.
zad. 5
przekrój osiowy walca jest kwadratem o boku długości 16. oblicz pole powierzchni bocznej tego
ostrosłupa.
zad.6
dany jest ostrosłup prawidłowy trójkatny o wszystkich krawedziach rownych 9. wyznaczdługosc
wysokosci tego ostrosłupa.
zad. 7
przekatna prostopadłoscianu jest nachylona do płaszczyzny podstawy pod katem 60 stopni.
podstawa prostopadłoscianu jest kwadratem o boku 3. wyznacz pole powierzchni całkowitej tego
prostopadłoscianu.
zad.8
tworzaca stozka jest o 2 dłuzsza od promienia jego podstawy.pole powierzhni bocznej stozka jest
rowne 120π. wyznacz objetosc tego stozka.
zad. 1
oblicz sinusa kata miedzy przekątną szescianu, a jego płaszczyzna podstawy.nic wiecej nie jest
podane. (rysunek)
zad. 2
ile scian i ile krawedzi ma ostrosłup o 20 wierzchołkach?
zad.3
Wszystkie krawedzie ostrosłupa prawidłowego czworokatnego maja jednakowa długość. Oblicz
objętosc ostrosłupa.
zad. 4
oblicz długosc przekatnej szescianu o krawedzi 12 cm.
zad. 5
przekrój osiowy walca jest kwadratem o boku długości 16. oblicz pole powierzchni bocznej tego
ostrosłupa.
zad.6
dany jest ostrosłup prawidłowy trójkatny o wszystkich krawedziach rownych 9. wyznaczdługosc
wysokosci tego ostrosłupa.
zad. 7
przekatna prostopadłoscianu jest nachylona do płaszczyzny podstawy pod katem 60 stopni.
podstawa prostopadłoscianu jest kwadratem o boku 3. wyznacz pole powierzchni całkowitej tego
prostopadłoscianu.
zad.8
tworzaca stozka jest o 2 dłuzsza od promienia jego podstawy.pole powierzhni bocznej stozka jest
rowne 120π. wyznacz objetosc tego stozka.
| a | 1 | √3 | ||||
sinα = | = | = | ||||
| a√3 | √3 | 3 |
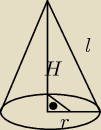 8. l=r+2
Pb=120π
Pb=πrl=πr(r+2)
πr(r+2)=120π
r2+2r−120=0
Δ=484 ⇒√Δ=22
( r=−10 ⋁ r=10 ) ⋀ r>0 ⇒r=10
V=13πr2H
H obliczysz z tw. Pitagorasa
8. l=r+2
Pb=120π
Pb=πrl=πr(r+2)
πr(r+2)=120π
r2+2r−120=0
Δ=484 ⇒√Δ=22
( r=−10 ⋁ r=10 ) ⋀ r>0 ⇒r=10
V=13πr2H
H obliczysz z tw. Pitagorasa
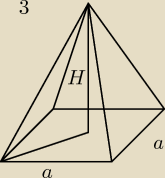 2.
ściany = wierzchołki
krawędzie : 46
3.
2.
ściany = wierzchołki
krawędzie : 46
3.
| 1 | ||
H2 + ( | a√2)2 = a2 | |
| 2 |
| 1 | ||
V = | * a2 * H | |
| 3 |
| H | ||
7. tg60 = | , a=3 | |
| a√2 |
| 1 | ||
V = | * πr2H mając to łatwo dojść do rozwiązania | |
| 3 |