zad matthew: Cześć, mam takie zadanie:

	π		π		√6
Rozwiąż równanie: sin(x+		) + sin(x −		) = −		dla x∊<0,2π>
	6		6		2

nie do końca wiem jak zabrać sie za to zadanie... mam rozbić jeden i drugi sinus na dwa równania?

	π		√6
bo gdybym mial cos takiego sin(x+		) = −		to pewnie dalbym sobie radę, ale tutaj
	6		2

mam problem .... proszę o pomoc...

Jack: Może z tego:

	α+β		α−β
sinα+sinβ=2sin(		)*cos(		)
	2		2

matthew: w dalszym ciągu nie wiem jak sie za to zabrac.... mozesz mi to jakoś rozpisać... tzn, ze moj sposob, gdzie rozbiłbym równanie na dwa jest zły? dzieki za odpowiedz

matthew: nie mam takiego wzoru... chociaż chyba sin(α+β) = sinαcosβ + cosβsinα...... to jest to samo?

Jack:

	2x		π		1		√6
2sin(		)*cos(		*		)=−
	2		3		2		2

	π		1
sin(x)*cos(		*		)=−√6
	3		2

	π		√6
sin(x)*cos(		)=−
	6		4

	√3		√6
sinx*		=−
	2		4

	√6*2		2√2		√2
sinx=−		=−		=−
	4√3		4		2

	π		5π
x= π+		=
	4		4

Jack: http://pl.wikipedia.org/wiki/Tożsamości_trygonometryczne#Suma_i_r.C3.B3.C5.BCnica_funkcji

matthew: ok juz wszystko jasne. dzieki Dany jest okrąg o równaniu x² + y² + 6x − 4y = 12. Wyznacz równanie stycznych do okręgu

	1
prostopadłych do prostej k: y =		x − 5.
	3

obliczyłem, że S = (−3,2) r = 5

	1
a także mam prostą || do prostej k przechodzącej przez punkt S, a jest nią y =		x + 3
	3

mam również prostopadłą do prostej k, jest nią y = −3x +b nie wiem jak zastosować tą prostą równoległą... Wiem, że muszę z niej skorzystać, jeżli chcę obliczyć te punkty okegu styczne z prostopadłymi do k, ale nie wiem jak... proszę o pomoc...

Godzio: y = −3x + b x² + y² + 6x − 4y = 12 => podstaw za y tą prostą, wylicz deltę jak wiemy fakt styczności sprawia że Δ = 0 => w ten sposób otrzymasz ab² + cb +d = 0 wyliczysz z tego Δ_b i pierwiastki i w ten sposób otrzymasz: y = −3x + b₁ y = −3x + b₂ jak nie dasz rady to pomogę

matthew: a nie da sie tych punktów obliczyć przy pomocy prostej równoległej? wtedy i jeden i drugi punkt podstawiłbym do prostej i otrzymałbym dwie proste styczne do okregu....

Godzio: hmmm być może ale takim sposobem jeszcze nie robiłem ale zaraz coś pokombinuje

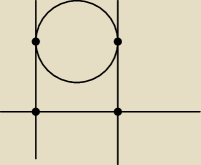
Godzio: Twój sposób chyba jest poprawny ale jest w nim ze 100razy więcej liczenia: 1. trzeba obliczyć te punkty stycznosci prostej równoległej przechodzącej przez środek: a w

	−30+3√130		−30−3√130
nich juz mi wyszly x1 =		x2 =
	10		10

do tego jeszcze trzeba by bylo y₁ i y₂ doliczyć. a dalej to trzeba znalesc proste prostopadle przechodzace przez te 2 punkty więc lepiej polecam mój sposób

Godzio: Myślę że tak jest łatwiej x² + (b−3x)² + 6x − 4(b−3x) − 12 = 0 x² + b² − 6b * x + 9x² + 6x − 4b + 12x − 12 = 0 10x² + x(18 − 6b) + b² − 4b − 12 = 0 Δ = (18−6b)² − 40(b² − 4b − 12) = 324 − 216b + 36b² − 40b² + 160b + 480 = −4b² − 56b + 804 = 0 /:(−4) b² + 14b − 201 = 0 Δ_b = 1000 √Δ_b = 10√10

	−14+10√10
b1 =		= − 7 + 5√10
	2

	−14 − 10√10
b2 =		= − 7 − 5√10
	2

matthew: chyba masz racje zdecydowanie lepszy

matthew: mam jeszcze takie zadanie:

	1
wyznacz dziedzinę funkcji f(x) = log3x+1(x3−x) −
	4x −8

(x³ − x) > 0 x(x² −1) > 0 x = 0 x = 1 x = −1 D∊(0,+∞) / {1}

	1
nie jestem pewny, poieważ zastanawiam sie, czy		również trzeba wziąć pod uwagę
	4x −8

proszę o sprawdzenie

Godzio: wszystko trzeba brać pod uwagę log_ab a>0 i a ≠ 1 b > 0 3x + 1 > 0 3x + 1 ≠ 1 x³ − x > 0 4^x − 8 ≠ 0 rozpisz to, podaj tylko wynik , ja Ci go sprawdze a jak coś naniesiemy poprawki

matthew: no dobra x³ − x > 0 to podałem juz na górze natomiast 4^x − 8 ≠ 0 4^x ≠ 8 (2²)^x ≠ 2³ 2^2x ≠ 2³ 2x ≠ 3

	3
x ≠
	2

3x + 1 > 0 ale tego nie muszę rozpisywać, bo przecież podstawa "a" nie liczy sie do dziedziny.... tak mi nauczyciel mowil

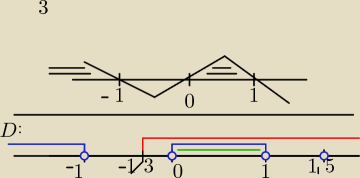
Godzio: To jednak napisze, a musze Cię zmartwić bo a również wlicza się do D, przy x³ − x popełniłeś błąd 1) 3x > − 1

	1
x > −
	3

2) 3x + 1 ≠ 1 x ≠ 0 3) x³ − x > 0 x(x−1)(x+1) > 0 x∊(−∞,−1) ∪ (0,1) 4^x ≠ 8 2^2x ≠ 2³ 2x ≠ 3

	3
x ≠		= 1,5
	2

D = (0,1) (zielone)

matthew:

	3
D∊ (0,+∞) / {1,		} ?
	2

matthew: masz racje wszystkie pierwiastki sa jednokrotne, ale liczba przy najwyzszej potedze jest dodatnia, wiec trzeba chyba od gory zaczac szkicowac wykres...

matthew: nie chce sie tutaj wymądrzać, ale zawsze jak liczyłem dziedzinę w logarytmach wystarczyło tylko obliczyć b, podstawę zostawiając w spokoju... dlatego jestem troche zaskoczony

Godzio: no tak odruchowo jakoś od dołu popraw i zaznacz na osi

Godzio: a co do "a" to najczęściej zawiera sie w b takze wyliczenie tego nic nie da ale np: log_x−5x+8 x+8 > 0 x > − 8 => x = −7,−6 => x−5 => −6−5 = −11 a nie istnieje taki logarytm : log₋₁₁2 prawda ?

matthew: racja, wiesz co ja chyba mowilem caly czas o takim logarytmie, np: log₃(x² −1) wtedy z podstawą nic nie trzeba kombinować

matthew: mam jeszcze jedno zadanie z parametrami: Dany jest trójmian kwadratowy f(x) = (m−2)x² + mx + 3. Wyznacz wszystkie wartości parametru m, dla których suma pierwiastków tego trójmianu jest wieksza od liczby przeciwnej do ich iloczynów. chodzi mi tylko o cześć zadania, którą nie jestem pewnien, czy dobrze zintrerpretowałem.... dla których suma pierwiastków tego trójmianu jest wieksza od liczby przeciwnej do ich iloczynów.

	1
mam to rozumiec w ten sposób: x1 + x2 >		?
	x1*x2

matthew: czy może tak: x₁ + x₂ > −(x₁*x₂) ?

Jack: przeciwna czyli ze znakiem przeciwnym, ta ostatnia propozycja jest dobra

matthew: acha i jeszcze jedno.... chodzi mi o delte, mam obliczyć wszystkie przypadki? tzn. Δ>0; Δ = 0; Δ<0 ?

matthew: aha *

Godzio: Δ > 0 tylko to Ciebie interesuje (i pamiętaj (m−2) ≠ 0 )

matthew: tak wiem ok, ale w takim razie dlaczego?

matthew: mam takie zadanie: Wykaż, że nie istnieje liczba m, taka że prosta o równaniu: y = (m² +m)x −1 jest nachylona do osi OX pod kątem 120² i tak, wiedzą że a = tgα tg120² = tg(180^o − 60^o) = −tg60^o = −tg√3 a = − √3 i dalej nie wiem proszę o pomoc

zajączek: a= m²+m m²+m= −√3 m²+m +√3=0 Δ= 1−4√3 <0 , m −−− nie istnieje

matthew: jak na to wpadałaś ze trzeba przyrównać jedno do drugiego? ogolnie wiem, że m2+m to jest wspołczynnik kierunkowy i że to jest faktycznie a.... wiesz co ja robilem... wstawialem obliczony współczynnik własnie za m2+m.... ech

zajączek: