PROSZĘ O POMOC !!! :( Wojtek: W trójkącie prostokątnym przyprostokątne mają długość 12cm i 5cm. Przez wierzchołek kąta prostego poprowadzono prostą, która podzieliła ten trójkąt na dwa trójkąty o równych obwodach. Oblicz stosunek długości promieni okręgów wpisanych w powstałe trójkąty.

Wojtek: ..........

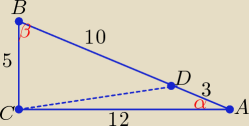
Bogdan: |AC| = 12, |BC| = 5, |AB| = √12² + 5² = 13 |BC| + |CD| + |DB| = |CA| + |AD| + |CD| ⇒ 5 + |DB| = 12 + 13 − |DB| ⇒ 2|DB| = 20 |DB| = 10, |AD| = 3

	5		12
sinα =		, sinβ =
	13		13

	1		12		300
Pole PBCD =		*5*10*sinβ = 25*		=
	2		13		13

	1		5		90
Pole PCAD =		*12*3*sinα = 18*		=
	2		13		13

r_B − długość promienia okręgu wpisanego w trójkąt BCD, r_A − długość promienia okręgu wpisanego w trójkąt CAD, p = połowa obwodu trójkąta BCD = połowa obwodu trójkąta CAD. P_BCD = r_B * p, P_CAD = r_A * p

	PBCD		PCAD
rB =		, rA =		,
	p		p

rB		PBCD     p		PBCD
	=		=
rA		PCAD     p		PCAD

rB		300     13		300
	=		=		= .....
rA		90     13		90