Oblicz współrzędne magda18: Punkty A=(−1,4), B=(5,−2), C=(7,2) są kolejnymi wierzchołkami równoległoboku ABCD. Oblicz współrzędne wierzchołka D tego równoległoboku.

Godzio: pomoge

Godzio: prosta AC : 2 = 7a + b 4 = −a + b − −−−−−−−−−−−−− −2 = 8a

	1
a = −
	4

prosta BD jest równoległa do AC i przechodzi przez B

	1
−2 = −		* 5 + b
	4

	5
−2 = −		+b
	4

	3
b = −
	4

	1		3
y = −		x −
	4		4

prosta AB: −2 = 5a + b 4 = −a + b − −−−−−−−−−−−−−−−−− −6 = 6a a = −1 b = 3 prosta CD jest równoległa do AB i przechodzi przez C: 2 = −1 * 7 + b 9 = b y = −x + 9 punkt przecięcia prostej CD i BD da nam punkt D y = −x + 9

	1		3
y = −		x −
	4		4

	1		3
−		x −		= −x + 9
	4		4

−x − 3 = −4x + 36 3x = 39 x = 13 y = −4

Gustlik: Godzio, sprawdź kolejność punktów, bo wg mnie trzeba zacząć do A i potem odliczać odwrotnie do ruchu wskazówek zegara, a więc równoległe są boki AB i DC, chyba zamieniłeś punkty C i D. Najlepiej to zrobić z wektorów: A=(−1,4) B=(5,−2) C=(7,2) D=(x, y) AB^→ = B − A = [5−(−1), −2−4] = [6, −6] DC^→ = AB^→ = [6, −6] − wektor ten jest równoległy i równy AB^→. DC^→ = C − D = [7−x, 2−y] Przyrównujemy współrzędne wektorów DC^→ i AB^→. 7−x=6 2−y=−6 −x=6−7 −y=−6−2 −x=−1 −y=−8 x=1 y=8 Zatem D=(1, 8).

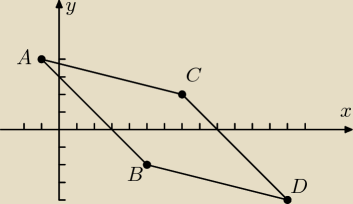
Godzio: rzeczywiście pomieszały mi się boki ale równoległobok też jest prawda ?

Gustlik: Jest to równoległobok, ale przy Twojej numeracji tez prościej byłoby to rozwiązać z wektorow − AB^→=CD^→ Czyli CD^→ = D − C = [x−7, y−2] = [6, −6] Mamy więc: x−7=6 i y−2=−6 x=13 y=−4 Czyli D=(13, −4).

ja: sex

Paula: czyli co jest dobrze rozwiazane? xD

ryśek: t