oblicz wyskość
magda: Oblicz wysokość CD trójkąta ABC, gdy IABI=6, IBCI=7, ICAI=5
29 mar 17:28
Ala:
Skoro AB = 6 a wysokosc dzieli go na pol to z jednej i drugiej strony ma po 3. Liczymy z
pitagorasa
a
2+b
2=c
2
3
2+b
2=7
2
9+b
2=25
b
2=25−9
b
2=16
b=
√16
b=4
ODP: Wysokosc CD wynosi 4
29 mar 18:31
Marcin: Rozwiązanie zgodne z rysunkiem jaki zrobiła wyżej Ala.
Obliczenia obarczone są błędem zaokrąglenia ( zaokrąglałem do 2−go miejsca po przecinku ).
1. Używasz wzoru Herona do obliczenia powierzchni trójkąta:
P = √p(p−a)(p−b)(p−c)
p = a + b + c / 2
a,b,c = boki trójkąta
P ~ 14,7 [j2}
2. Następnie ze wzoru na ... pole trójkąta obliczasz:
P = CD * AB * 1/2
14,7 = CD * 6 * 1/3
4,9 = CD = h
29 mar 18:45
Ala: nie sadze zeby to bylo az tak skomplikowane ...zeby uzywac jakis wzorow Herona.... magda w
ktorej klasie jestes?
29 mar 18:55
magda18: w drugiej
29 mar 19:07
Ala: gim czy liceum?
29 mar 19:28
Bildorf:
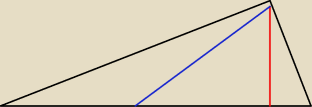
wysokosc CD musi byc linia rownolegla do AB wiec nie mozna sobie wyznaczyc polowy z odcinka na
przeciwko, patrz linia niebieska
29 mar 22:27
Bogdan:
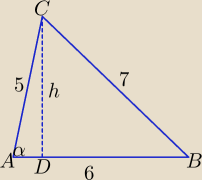
Można np. tak:
| | 61 − 49 | | 1 | |
Z tw. cosinusów w trójkącie ABC: 49 = 25 + 36 − 60cosα ⇒ cosα = |
| = |
| |
| | 60 | | 5 | |
| | 1 | |
W trójkącie ADC: jeśli cosα = |
| , to |AD| = 1 i h = √25 − 1 = ... |
| | 5 | |
18 wrz 21:11