monotoniczność funkcji Nikka:

	2
Wskaż zbiór, w którym funkcja f(x) = −		jest rosnąca.
	x

a. R\{0} b. R\{2} c. (2,∞) d. (−∞,2) prawidłowa odpowiedź to c. a mnie wychodzi a. mój błąd czy błąd w odpowiedziach Będę wdzięczna za rozwianie wątpliwości.

Bogdan:

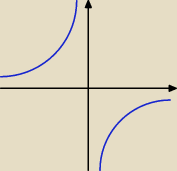
	2
Funkcja f(x) = −		jest rosnąca dla x ∊ (−∞, 0), (0, +∞).
	x

Ten zapis nie jest równoznaczny z zapisem x ∊ R \ {0}. Zapis: x ∊ R \ {0} jest równoznaczny z zapisem: x ∊ (−∞, 0)∪(0, +∞). Przy opisywaniu przedziałów monotoniczności nie wstawia się znaku sumy zbiorów, można wstawić przecinek. Żadna z odpowiedzi nie jest prawidłowa.

Nikka: Rozumiem, tyle, że jako prawidłową odpowiedź podają c. Funkcja jest rosnąca w przedziałach (−∞,0) i (0,∞). Może autorowi chodziło o to, że przedział (2,∞) ⊂ (0,∞) i dlatego c.

Bogdan: Można uznać taka interpretację, funkcja jest bez wątpienia rosnąca w przedziale (2, ∞), tym bardziej, że brak w zadaniu polecenia: wskaż maksymalne przedziały, w których funkcja jest rosnąca.

Jack: Zauważ jednak, że licząc pochodne zapisuje się np. tak:

	2
f'(x)=
	x2

f(x)↗ gdy: f'(x)>0 ⇔ x≠0 ⇔ x∊R\{0} Wówczas zapisuje się, że funkcja f(x) rośnie dla f'(x)>0 czyli gdy x∊R\{0}. Wydaje mi się, że zapis je R\{0} jest w porządku.

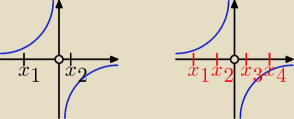
Bogdan: Do Jack. Przyjmijmy, że f↗ dla x ∊ R \ {0} Z definicji funkcji rosnącej: funkcja f(x) jest rosnąca w zbiorze A wtedy, gdy dla każdego x₁, x₂ ∊ A z założenia x₂ − x₁ > 0 wynika f(x₂) − f(x₁) > 0. Widać na rysunku, że: x₁, x₂ ∊ R \ {0} i x₂ > x₁ ⇒ x₂ − x₁ > 0. Widać również, że f(x₂) < f(x₁) ⇒ f(x₂) − f(x₁) < 0, co jest niezgodne z definicją funkcji rosnącej. Nie można więc powiedzieć, że f↗ dla x ∊ R \ {0}. Należy natomiast stwierdzić, że f↗ dla x ∊ (−∞, 0), (0, +∞), teraz definicja jest spełniona. Dla każdego x₁, x₂ ∊ (−∞, 0) i x₂ − x₁ > 0 jest f(x₂) − f(x₁) > 0. Dla każdego x₃, x₄ ∊ (0, +∞) i x₄ − x₃ > 0 jest f(x₄) − f(x₃) > 0.

zajączek: A jeżeli podamy taką odp: f(x) rosnąca w całej dziedzinie

Bogdan: Dziedziną funkcji przedstawionej na rysunku jest R \ {0}, stwierdzenie − funkcja jest rosnąca w całej dziedzinie oznaczałoby, że jest rosnąca w zbiorze R \ {0}, co prowadzi do sprzeczności z definicją funkcji rosnącej. Nie można więc powiedzieć w każdym przypadku, że funkcja jest rosnąca w całej dziedzinie. Można użyć takiego sformułowania dla niektórych funkcji, np. dla funkcji f(x) = 3x, f(x) = √x, f(x) = x³.