Stosunek promieni Paweł: Dane są 2 okręgi styczne zewnętrznie. Wspólne styczne tych okręgów przecinają się pod kątem α. Oblicz stosunek promieni tych okręgów.

Paweł: odswiezam

Bogdan:

r		α		r
	= sin		⇒ a =
a		2		α   sin   2

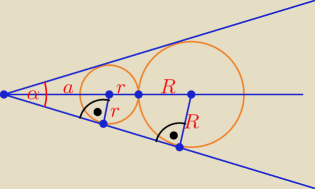
R		α		α		α		α
	= sin		⇒ R = Rsin		+ rsin		+ asin
R + r + a		2		2		2		2

	α		α		r		α
R = Rsin		+ rsin		+		*sin
	2		2		α   sin   2		2

α

α

R

R

α

α

R = Rsin

+ rsin

+ r / :r ⇒

−

sin

= sin

+ 1

2

2

r

r

2

2

R		α		α
	(1 − sin		) = 1 + sin
r		2		2

R		α   1 + sin   2
	=		= k
r		α   1 − sin   2

Można kontynuować:

	π   α   sin + sin   2   2
k =		=
	π   α   sin − sin   2   2

	π + α   π − α   2sin cos   4   4
=		=
	π − α   π + α   2sin cos   4   4

	π + α		π − α
= tg		tg
	4		4

Paweł: Dzięki !

Anka: Czy istnieje jeszcze inny sposób obliczania tego zadania?

Jack: to bardzo dobry sposób. Nie wiem czy coś nowego wniosę ale można wszystko sprowadzić do dwóch równań (i rysunku Bogdana).

a		a+r+R
	=		(z podobieństwa trójkątów)
2r		2R

	α		r		r
sin		=		⇒ a=		(z funkcji znanego kąta α)
	2		a		α   sin   2

Teraz tylko podstawić i wyznaczyć stosunek R/r albo odwrotnie.