czy wysokość = średnicy? jakoś zależność z promienia trzeba wykorzystać? Sara: W trapez równoramienny wpisano okrąg, którego średnica ma długość 9 cm. Obwód trapezu jest równy 60 cm. Oblicz: a) pole trapezu b) długości boków trapezu c) sinus kata ostrego przecięcia przekątnych tego trapezu

Godzio: pomoge

aga: tak h=2r można tez skorzystać z zalezności o okręgu wpisanym w czworokąt "sumy długości przeciwległych boków są równe ". w naszym przypadku a+b=2x (jesli a i b to podstawy, a X ramiona)

Godzio: a+b = 2c a+b + 2c = 60 4c = 60 c = 15

	(b−a)2
c2 = h2 +
	4

900 = 324 + (b−a)² (b−a)² = 576 b−a = 24 a+b = 30 −a+b = 24 + −−−−−−−−−−−−−−− 2b = 54 b = 27 a = 3

	a+b
P =		* h
	2

dokończ zaraz sin

aga: połączyć to z równaniem z wykorzystaniem obwodu i wyliczyć najpierw sumę a+b, co pozwoli nam obliczyć już pole. to byłby podpunkt a).

Sara: 270 cm² mi wyszło pole

Godzio: c) sinus kata ostrego przecięcia przekątnych tego trapezu √9²+15² = x x = 3√34

9		y
	=
15		13,5

y = 8,1 y² + 13,5² = z² z = √247,86 z = 2,7√34 3√34 − 2,7√34 = 0,3√34 i z tw cos 15² = (0,3√34)² + (2,7√34)² − 2 * 0,3√34*2,7√34*cosα 225 = 3,06 + 247,86 − 55,08cosα 25,92 = 55,08cosα

	8
cosα =
	17

cos²α + sin²α = 1

64
	+ sin2α = 1
289

	225
sin2α =
	289

	15
sinα =
	17

sorki że tak skomplikowanie ale innego pomysłu nie mam

Sara: ⁹₁₅=^y_13,5 − a skąd wiadomo, że będzie 13,5?

Sara: jaaa strasznie to zagmatwałeś, ale dojdę to twojego wyniku oczywiście dziękuję bardzo aga też dzięki!

Godzio: 3 = 2x x = 1,5 15 − 1,5 = 13,5

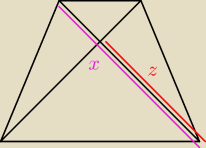
Godzio: założe się że to banalne ale coś nie moge na to wpaść napisze Ci tylko co jest czym , reszte chyba powinnaś wiedzieć co czym jest

Sara: aha faktycznie bo "a" wcześniej obliczyliśmy, ok