walec Maturzysta: walec i przekrój płaszczyzny przez dowolny punkt A okręgu górnej podstawy walca poprowadzono przekrój płaszczyzna zawierajacą oś walca. W dolnej podstawie walca poprowadzono średnicę BC, prostopadła do przekroju osiowego. Promień podstawy walca ma długosc r oraz kąt BAC =α , gdzie α(0,

	π
		).
	2

Wykonaj rysunek i oblicz objętość. Proszę o pomoc

	r3π
wyszło mi		jednak w odp jest inny wynik. Jest jeszcze pierwiastek z tangensem
	tg (α/2)

w liczniku proszę o pomoc

Anna: pomagam

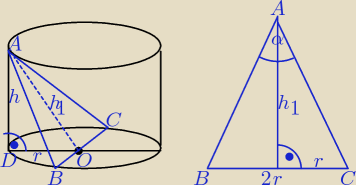
Anna: Dane: r, α , V = ? V = πr²h

	r		α
		= tg
	h1		2

	r
h1 =
	α   tg   2

Z ΔADO : h² + r² = h₁² h² = h₁² − r²

	r2
h2 =		− r2
	α   tg2   2

	α   r2−r2tg2   2
h2 =
	α   tg2   2

	r		α
h =		*√1−tg2
	α   tg   2		2

	r		α		α   πr3√1−tg2   2
V = πr2 *		*√1−tg2		=
	α   tg   2		2		α   tg   2

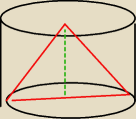
Maturzysta: wszystko sie zgadza lecz skad wiesz ze taki bedzie rysunek a nie np taki :

Reaven: "przez dowolny punkt A okręgu górnej podstawy walca" wiec punkt A nie moze byc na srodku górnej podstawy

Anna:

: a w ktorym miejscu przekroj zawiera os?

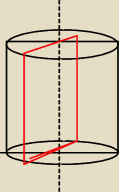
Basia: skoro ma przechodzić przez oś walca i punkt na okręgu musi być tożsamy z przekrojem osiowym i jest po prostu prostokątem

Basia: okręgu Reaven; nie koła

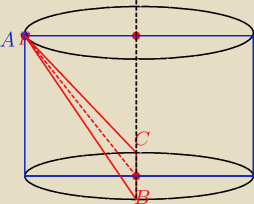
Basia: ale dalej oczywiście będzie ten trójkąt, który narysowała Anna A zaznaczamy tak dla wygody; przecież zawsze mogę walce obrócić Przekrój to ten niebieski prostokąt

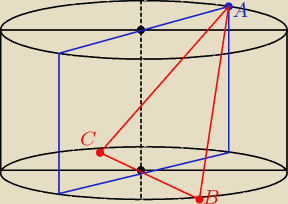
Basia: a ten rysunek już powinien rozwiać wszystkie wątpliwości