ostrosłupy judyta: Oblicz pole powierzchni całkowitej ostrosłupa prawidłowego trójkątnego, którego krawędź boczna ma długość 4 cm, a krawędź podstawy jest równa 6 cm.

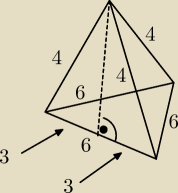
Madzia: Pc = Pp + 3*P ściany bocznej

	62√3
Pp =		= 9√3
	4

P ściany bocznej = 6 * wys. ściany Wysokość tę można obliczyć z tw. Pitagorasa, ponieważ dzieli ona bok długości 6 cm na pół.

Madzia: Pomyliłam się, pole ściany bocznej powinno mieć postać: P ściany bocznej = 1/2 * 6 * h = 3 * h h² + 3² = 4² h = √5 P ściany bocznej = 3√5 Pc = Pp + 3*P ściany bocznej Pc = 9√3 + 9√5 = 9*( √3 + √5 ) Chyba teraz powinno być dobrze

Bogdan:

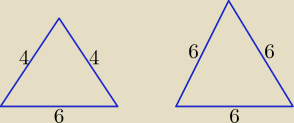
	1
Ściana boczna: p =		(4 + 4 + 6) = 7, p − 4 = 3, p − 6 = 1
	2

Pole ściany bocznej z wzoru Herona P_Δ = √7 * 3 * 3 * 1 = 3√7

	1
Pole podstawy PP =		*62√3 = 9√3
	4

Pole powierzchni całkowitej ostrosłupa P_C = 3 * P_Δ + P_P = 9√7 + 9√3 = 9(√7 + √3)