Funkcja Homograficzna Silwest: Wyznacz zbior wartosci funkcji f(x)= ^2|x|−1_|x|+1 no nie moge takie proste a nie moge dojsc do odpowiedzi ktora jest <−1;2)

Nikka: może najpierw należy rozbić podaną funkcję na dwa przypadki tzn. dla x ≥ 0 i x < 0

Madzia: Mi również nie wychodzi taka odpowiedź. Czy jest ona na pewno prawidłowa?

Silwest: Nikka ... zauważ ze nawet gdy x< 0 to przeciez i tak wartosc bezwzgledna jest ... to i tak i tak jest tylko 1 wzor taki glowny bez modułów Madzia no wlasnie jest to ksiazka i chyba powinno byc prawidlowo choc juz 1 blad w niej znalazlem ale nie wiem rly ...

Julek: dla x ∊ (−∞;0)

	−2x − 1		2x + 1		2(x−1) + 3		3
f(x) =		=		=		= 2 +
	−x+1		x − 1		x−1		x−1

Narysuj to i odczytaj zbiór wartości f(x), ale tylko dla x < 0, co będzie zbiorem A dla x ∊<0;+∞)

	2x − 1		2(x+1) − 3		3
f(x) =		=		= 2 −
	x+1		x+1		x+1

Narysuj to i odczytaj zbiór wartości f(x), ale tylko dla x ≥ 0, co będzie zbiorem B Zw = A ∪ B

Madzia: Według mnie zborem wartości powinien być R−{2}. U mnie w zbiorze zadań są również błędy, może ta odpowiedź jest błędna. Mimo wszystko ja bym dała odp. R−{2}

Silwest: Julek przeciez nie moze byc zbior od −nieskonczonosci do zera zadna liczba podstawiona pod x nie da liczby ujemnej z 2 sie zgadzam

Silwest: Madzia juz troche ogarniam na poczatku tez bym tak powiedzial ale nie Bo przeciez jest to Wartos bezwzgledna czyli musimy odbic od osi OX ale i tak wychodzi mi od <0; do nieskonczonosci)

Madzia: Ale wartość bezwzględna jest tylko na argumencie, nie na całości, czyli odbicie względem osi OY. To i tak daje całe R bez asymptoty y = 2.

Nikka: czyli dobrze myślałam A = (−1,2) B = <−1,2) A∪B = <−1,2)

	a
a czy można w tym zadaniu wykorzystać informację, że Zw = R \{		} ?
	c

Nikka: R\{2} byłoby Zw gdybyśmy nie mieli modułu − tak mi się wydaje − a tu w każdym z przypadków rysujemy tylko fragment funkcji i faktycznie na wykresie jaki sobie narysowałam wychodzi <−1,2)

Silwest: No ale nie rozumiem jak moze tak byc jak julek napisal przeciez |x| nawet gdy x< 0 to i tak jest x>0 .... nie ogarniam

Madzia: Nikka Julek chyba rzeczywiście macie rację. Nie wiedziałam, że w przypadku modułu nie można skorzystać z Zw = R−{a/c}

Nikka: Julek korzystał z definicji wartości bezwzględnej − i tu inaczej się nie da bo funkcja ma inną postać dla x ≥ 0 i inną dla x < 0.

Silwest: no raczej nie ma innej wartosci bo jak bedzie ... za x= − 2 no to co przeciez wartosc bezwzgledna z −2 to i tak 2

Tomek.Noah: jak brzmi zasada wartosci bezwzglednej ze to co w module jest albo wieksze od zera albo mniejsze i wlasnie opuszczajc te moduly rozpatrujesz te warunki...

Nikka: Def. |x| = x dla x ≥ 0 |x| = −x dla x < 0 z def. wynika, że |x| ≥ 0 tyle, że we wzorze funkcji nie może zostać |x|, dlatego rozważamy dwa przypadki zgodnie z def. ...

Jack: f. jest parzysta wiec symetryczna względem OY. Wystarczy zbadać co sie dzieje dla x≥0.

	3		−3
f(x)=2−		(na podstawie wyliczeń Julka. Zatem mamy funkcję g(x)=
	x+1		x

przeniesioną o wektor [−1,2] Po pierwsze g(x) jest to funkcja rosnąca dla x≥0, wiec obraz dla x<0 będzie malejący. Po drugie w granicy x→∞ będzie g(x)=0, więc dla x→∞ będzie f(x)=2. Skoro g(x) jest rosnąca, to f(x) też (jako zwykle przesunięcie o wektor). Stąd najmnijesza wartość będzie dla x=0 (na brzegu przedziału), czyli f(0)=−1. Więc zb_f(x)= <−1,2>.

Jack: sory, 2 jest w granicy więc oczywiscie zb_f(x)=<−1,2).

Silwest: No nie moge tego pojać .. .

mielonka: f(x)=x=2/x+1

mielonka: czy ktoś umie rozwiązać funkcję homograficzną pomocy

Bogdan:

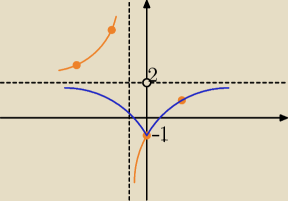
	2x − 1		−3
g(x) =		⇒ g(x) =		+ 2, (pomarańczowy wykres)
	x + 1		x + 1

	|x| − 1
f(x) =		, (niebieski wykres), y∊<−1, 2)
	|x| + 1

Grześ: a ja pokażę sposób algebraiczny bez rysowania wykresów. Jeśli ktoś jest zainteresowany.

	2|x|−1
Wyznaczenie zbioru wartości funkcji f(x)=		, to ułożyć takie równanie:
	|x|+1

2|x|−1
	=p, które dla p∊R, ma choć jedno rozwiązanie
|x|+1

Znajdujemy wartości p: 2|x|−1=p|x|+p (2−p)|x|=p+1 dla p=2 mamy: 0*|x|=3, sprzeczność, czyli brak rozwiązań Teraz dla p≠2, dzielimy przez (2−p)

	p+1
|x|=
	2−p

Teraz to równanie ma rozwiązaniem tylko, gdy:

p+1
	≥0 p≠2
2−p

−(p+1)(p−2)≥0 (p+1)(p−2)≤2 p∊<−1,2) Czyli ZW=<−1,2) Jak ktoś zainteresowany, to sobie to przeanalizuje

Paulina: Wyznacz zbiór wartości funkcji f(x)= 4x/x²+1.

Lulek:

	⎧	x−4 jeśli x∊( −∞,1)
ile miejsc zerowych ma funkcja f(x) =	⎨
	⎩	12x jeśli x∊<1, +∞)

Krzysiek: x−4=0 to x=4 nalezy czy nie nalezy do przedzialu (−∞,1) 1/2x=0 to x=0 nalezy czy nie nalezy do przedzialu (<1,nieskon) No to ile jest miejsc zerowych ?

Atar1x: sposób Grzesia dobry!

ta co niewie: Wyznaczony zbiór wartości funkcji f

1
x2 + 2x−24

X należy do <−5,3>