A Marta: Dane są wierzchołki trójkąta: A = (2,2), B = (7,7), C = (10,3). Wyznacz długość wysokości trójkąta ABC opuszczonej z punktu C.

Marta: POMOCY

Madzia: Musisz najpierw obliczyć pole trójkąta ze wzoru P = 1/2 | (xb−xa)(yc−ya)−(yb−ya)(xc−xa)|. Potem oblicz długość podstawy, na którą opuszczona jest wysokość (czyli AB). Porównaj pola P = 1/2 | (xb−xa)(yc−ya)−(yb−ya)(xc−xa)| = 1/2 * a * h stąd wyliczysz h.

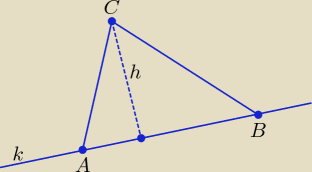
Bogdan: A = (2, 2), B = (7, 7), C = (10, 3) Najpierw trzeba wyznaczyć równanie prostej k: y = ax + b przechodzącej przez punkty A i B.

	5
a =		= 1, y = (x − 2) + 2 ⇒ y = x ⇒ x − y = 0.
	5

Teraz obliczamy odległość punktu C od prostej k, ta odległość jest równa h.

	|1*10 − 1*3|		7
h =		=
	√1 + 1		√2