PLANIMETRIA ?????????: Promień okręgu opisanego na trójkącie prostokątnym jest równy 12,5 a promień okręgu wpisanego w ten trójkąt jest równy 3. Oblicz pole tego trójkąta.

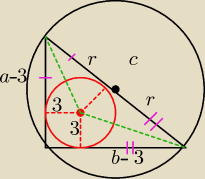
Jack: zielone linie to dwusieczne. Mamy więc że a−3=r oraz b−3=r (trójkąty przyległe) Wiemy, że promien okręgu opisanego do połowa przeciwprostokątnej, czyli 2r=c (2+12,5=25=c). Zatem a−3+b−3=25 a+b=36 Wiemy że to trójkąt prostokątny, więc a²+b²=c²=25² Dalej już prosto.

?????????: skąd się wzięło to 36?

Jack: no wlasnie, na ekranie pisałem... oczywiście masz rację, że zrobiłem błąd

Bogdan: a, b − długości przyprostokątnych, c − długość przeciwprostokątnej, c² = a² + b², R = 12,5 − długość promienia okręgu opisanego, c = 2R = 25, a² + b² = 25²,

	1
r = 3 − długość promienia okręgu wpisanego, r =		(a + b − c)
	2

	1
Pole P =		ab
	2

	1
3 =		(a + b − 25) ⇒ 6 = a + b − 25 ⇒ a + b = 31 / 2
	2

a² + b² + 2ab = 31² ⇒ c² + 2ab = 31² ⇒ 2ab = 31² − 25²

	ab
2ab = 336 /:4 ⇒		= 84
	2

Odp.: Pole P = 84.

zuzka062: oblicz długość promienia okręgu opisanego na trójkącie prostokątnym o przyprostokątnych długości 5 i 12. Proszę najepiej o jakiś rysunek

lols: