Ciagi Hashiri: Witam, Zad.1 Uzasadnij, ze w trojkacie prostokatnym wysokosc opuszczona z wierzcholka kata prostego jest srednia geometryczna dlugosci odcinkow, na jakie dzieli ona przeciwprostokatna. Zad.2 Wykaz, ze dla dowonlych liczb dodatnich x i y zachodzi taka zaleznosc :

x+y
	≥√xy
2

oraz kiedy te srednie sa rowne ? prosze o jak najszybsza pomoc

Godzio: (x+y)² = a² + b² h² + x² = a² h² + y² = b² − −−−−−−−−−−−−−−−−−−−−− x² + y² + 2xy = a² + b² x² − y² = a² − b² − −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 2y² + 2xy = 2b² y² + xy = b² y² + xy = h² + y² h² = xy h =√xy

Jack: 2. http://matematyka.pl/178221.htm

Godzio:

x+y
	≥ √xy /*2
2

x+y ≥ 2√xy /² x² + 2xy + y² ≥ 4xy x² − 2xy + y² ≥ 0 (x−y)² ≥ 0 każda liczba podniesiona do kwadratu jest większa równa zeru

Hashiri: Wow jak szybko Dzięki Znales ten dowod

Godzio: nie ale takie proste to łatwo dojść

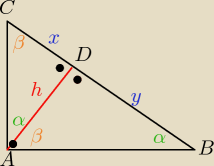
Eta: zad. 1)

	y		h
ΔABD ~ ΔADC to:		=
	h		x

to h²= x*y => h = √x*y c.n.u

Hashiri: Dzieki Mam jeszcze taki zadanie Suma trzech poczatkowych wyrazow ciagu geometrycznego jest rowna 21, a suma trzech nastepnych: 168.Ktory wyraz tego ciagu jest rowny 192

Hashiri: Prosze, niech mi ktos szybko to zrobi

Jack:

	21
a1+qa1+q2a1=21 ⇒ a1(1+q+q2)=21 ⇒ (1+q+q2)=		(□)
	a1

q³a₁+q⁴a₁+q⁵a₁=168 ⇒ a₁q³(1+q+q²)=168 podstaw (□) do drugiego równania i wylicz q. Potem skorzystaj ze wzoru na sumę (wiesz ile wynosi suma a₁+a₂+...+a₆).

Eta: można to uprościć, tak: a₁( 1+q+q²)=21 i a₁*q³(1+q+q²)= 168 to 21*q³= 168 => q³= 8 => q= 2 to a₁ (1+2+4)=21 => a₁=3

	3
an= 3*2n−1 =>		*2n= 192
	2

to: 2ⁿ= 128 => 2ⁿ= 2⁷ => n= 7 więc wyraz a₇= 192