Andrzej:
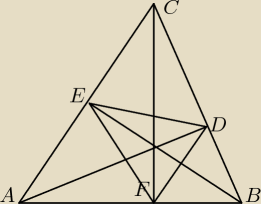
niech kąty A, B, C będą odpowiednio równe α,β,γ.
Wiadomo że ABC~DEC, więc kąt EDC = α, wtedy kąt ADE = 90−α
oraz ABC~DBF, więc kąt BDF = α, wtedy kąt ADF = 90−α
czyli DA jest dwusieczną kąta FDE.
Reszta analogicznie.
Aha, jeśli nie jest oczywiste to co napisałem na początku o tym podobieństwie to dowodzik:
ADC ~ BEC − kąt C wspólny i po jednym kącie prostym, cecha kk
stąd |DC| : |AC| = |EC| : |BC|, a przekształcając tę proporcję mamy
|DC| : |EC| = |AC| : |BC|, do tego dokładamy wspólny kąt C więc na podstawie cechy bkb
trójkąty ABC i DEC są podobne.
Ewa: Zrozumiałam i bardzo dziękuję Ci za pomoc

Tylko nie wiem dlaczego jest tak, że kąt EDC = α
a nie β czy γ ?
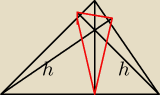 Bardzo Proszę o pomoc.
Bardzo Proszę o pomoc.  Jak uzasadnić że wysokości czarnego trójkąta to dwusieczne trójkąta czerwonego ? Bardzo proszę
o pomoc
Jak uzasadnić że wysokości czarnego trójkąta to dwusieczne trójkąta czerwonego ? Bardzo proszę
o pomoc 
 niech kąty A, B, C będą odpowiednio równe α,β,γ.
Wiadomo że ABC~DEC, więc kąt EDC = α, wtedy kąt ADE = 90−α
oraz ABC~DBF, więc kąt BDF = α, wtedy kąt ADF = 90−α
czyli DA jest dwusieczną kąta FDE.
Reszta analogicznie.
Aha, jeśli nie jest oczywiste to co napisałem na początku o tym podobieństwie to dowodzik:
ADC ~ BEC − kąt C wspólny i po jednym kącie prostym, cecha kk
stąd |DC| : |AC| = |EC| : |BC|, a przekształcając tę proporcję mamy
|DC| : |EC| = |AC| : |BC|, do tego dokładamy wspólny kąt C więc na podstawie cechy bkb
trójkąty ABC i DEC są podobne.
niech kąty A, B, C będą odpowiednio równe α,β,γ.
Wiadomo że ABC~DEC, więc kąt EDC = α, wtedy kąt ADE = 90−α
oraz ABC~DBF, więc kąt BDF = α, wtedy kąt ADF = 90−α
czyli DA jest dwusieczną kąta FDE.
Reszta analogicznie.
Aha, jeśli nie jest oczywiste to co napisałem na początku o tym podobieństwie to dowodzik:
ADC ~ BEC − kąt C wspólny i po jednym kącie prostym, cecha kk
stąd |DC| : |AC| = |EC| : |BC|, a przekształcając tę proporcję mamy
|DC| : |EC| = |AC| : |BC|, do tego dokładamy wspólny kąt C więc na podstawie cechy bkb
trójkąty ABC i DEC są podobne.
 Tylko nie wiem dlaczego jest tak, że kąt EDC = α
a nie β czy γ ?
Tylko nie wiem dlaczego jest tak, że kąt EDC = α
a nie β czy γ ?