Problem trygonometria brg2104: √3sinx + cosx=m Podobno można podzielić przez 2 i użyć wzoru na sinus sumy. Nie wiem jak to zrobić skoro wzór na sinus sumy ma postać : 2sin [(x+y)/2)] cos[(x−y)/2]

Godzio: jakie polecenie ?

brg2104: ' zbadaj dla jakich wartości parametru m istnieją rozwiązania rownania: ' Wystarczy zatem obliczyć zbiór wartości funkcji i przyrównać do niego m

Godzio: √3sinx + √1−sin²x = m √3sinx − m = √1−sin²x /² 3sin²x − 2√3m * sinx + m² −1 + sin²x = 0 4sin²x − 2√3msinx + m² −1 = 0 sinx = t t∊<−1,1> 4t² − 2√3m t + m² − 1 = 0 Δ > 0 Δ = 12m² − 16m² + 16 = −4m² + 4 > 0 −4m² + 4 > 0 /:(−4) m² − 1 < 0 m² < 1 m < 1 i m>−1 m∊(−1,1)

brg2104: m∊<−2;2> We wskazówce mam :'podziel obie strony równania przez 2 i skorzystaj ze wzoru na sinus sumy' Godzio, pamiętaj też że parametr m odnosi się do Zbioru wartości funkcji!

Godzio: dobrze jest tylko Δ = −4m² +16 ≥ 0 /:(−4) m² − 4 ≤ 0 m² ≤ 4 m≤2 i m ≥ −2 m∊<−2,2> a tej wskazówki w ogóle nie rozumiem

brg2104: też chyba przejde\ę na twój sposób thx.

Bogdan: √3sinx + cosx = m

	√3		1
y = √3sinx + cosx ⇒ y = 2(		sinx +		cosx) ⇒
	2		2

	π		π		π
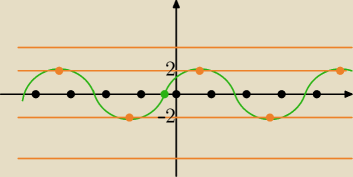
⇒ y = 2(sinx cos		+ sin		cosx) ⇒ y = 2sin(x +		) (zielony wykres)
	6		6		6

oraz y = m (fukcja stała, pomarańczowa linia) Równanie ma rozwiązania dla m ∊ <−2, 2>

Bishop: Robiąc zgodnie ze wskazówką: P{3}sinx + cosx = m /*2

√3		1		m
	sinx +		cosx =
2		2		2

	π		π		m
cos		*sinx + sin		*cosx =
	6		6		2

	π		m
sin(x +		) =
	6		2

m∊[−2,2]