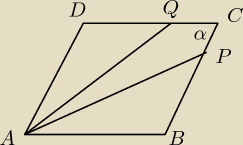
planimetria Sfrustrowany: Bardzo proszę o pomoc− wytłumaczenie. Romb ABCD o boku długości a i kącie ostrym α podzielono na trzy części o równych polach odcinkami AP oraz AQ (P∊ BC, Q∊ DC). Wyznacz długość odcinków AP oraz AQ. Domyslam sie, ze |AQ|=|AP| i ze moze byc cos ze wzorem na pole rombu tylko nie wiem co i jak

simple: wiemy, że |<BCD|=|<DAB|=α i |<ADC|=|<ABC|= 180 − α Pole ABCD = a*a*sinα więc Pole ΔADQ=1/3*a*a*sinα Pole ΔADQ to również a*|DQ|*sin(180−α) porównujesz te dwa wzory i wyliczasz długość |DQ| póżniej z twierdzenia cosinusów liczysz długość |AQ|. ΔADQ jest przystający do |APB| więć postępujesz analogicznie.

Sfrustrowany: dziekuje bardzo

Sfrustrowany : Moment bo cos mi nie idzie niech |AD|=|DC|=|BC|=|BA|=a w takim razie :

	1
PΔADQ=		PABDC
	3

	1		1
a*|DQ|*		*sin(180−α)=		*a*a*sinα
	2		3

	2
|DQ|=		a
	3

i teraz twierdzenie cos.

	4		2
|AQ|2=a2+		a2−2*cos(180−α)*		a2
	9		3

	4		4
|AQ|2=a2+		a2+		a2*cosα
	9		3

co dalej?:(

Sfrustrowany : ktoś posłuży radą?

Sfrustrowany: hmm?:(

Sfrustrowany: odswiezam

Jack: dodaj te ułamki, a policzysz |AQ|, cosα to znana wartość...

Sfrustrowany:

	13		4
|AQ|2=		a2+		a2cosα
	9		3

	1		13
|AQ|2=		a2(		+4cosα)
	3		3

jak cos to znana wartosc?

Nikka: a i α − przyjmuje się jako znane ( z treści zadania), mimo, że nie znamy wartości liczbowych to traktujemy jako wiadome...

Sfrustrowany: omg bez komentarza. Dzieki wielkie