wykaż że an: wiedząc że α i β są kątami ostrymi oraz sinα=1/√10 i tgβ=4/3 wykaż, że 2α+β=π/2 prośba o pomoc

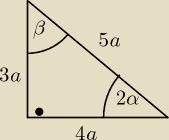
Jack: Policzysz, że: Dla kąta α:

	3√10		4		3
cosα=		oraz sinβ=		, cosβ=		.
	10		5		5

3√10		√10		sin2α
	*		=cosα*sinα=
10		10		2

3		sin2α
	=		⇒ sin2α=0,6 ⇒ cos2α=0,8 ⇒ α<45o (bo dla 2α>90o cos2α<0)
10		2

Teraz dla kąta β: Policzysz, że sinβ=0,8 oraz cosβ=0,6 Stąd mamy: sinβ=cos2α=0,8 Zróbmy rysunek: ... ... ...

	π
Z własności trójkąta mamy, że 2α+β=90o=
	2

Licząc również mamy:

3		4		12		sin2β		24
	*		=		=sinβ*cosβ=		⇒ sin2β=		=0,96.
5		5		25		2		25

	sin4α
0,6*0,8=		⇒ sin4α=0,96.
	2

	4α−2β		4α+2β
0=sin4α−sin2β=2sin(		)*cos(		) (□)
	2		2

0=sin(2α−β)*cos(2α+β)

	π
A więc (2α−β=0 lub 2α−β=π) lub 2α+β=
	2

a) Rozpiszmy nawias: 2α=β ⇒ sin2α=sinβ ⇔ 0,6=0,8 ⇒ sprzeczność

	π
b) gdy 2α−β=π ⇒ 2α=π+β ⇒ α>		⇔ sprzeczność
	2

	π		π
c) 2α=		−β ⇒ sin2α=sin(		−β) ⇔ sin2α =cosβ ⇔ 0,6=0,6.
	2		2

(nie prowadzi do sprzeczności, właściwie nie trzeba tej 3. możliwości sprawdzać) Trzecia ścieżka nie prowadzi do sprzeczności, a równość (□) jest prawdziwa dla

	π
2α+β=		.
	2

Koniec.

Eta: można też tak:

	1
sinα=
	√10

	3
cosα=
	√10

	6		3
sin2α= 2sinα*cosα=		=
	10		5

	4
cos2α=
	5

	cos2α		4		5		4
ctg2α=		=		*		=
	sin2α		5		3		3

i tgβ= ⁴₃ zatem ctg2α= ctg( ^π₂−β) => 2α= ^π₂−β => 2α+β= ^π₂