Zadanie Marzenka: Proszę kogoś o pomoc. W czworokątnym ostrosłupie prawidłowym kąt płaski przy wierzchołku równa się α, bok podstawy równa się a. Oblicz promień kuli opisanej na tym ostrosłupie.

Bogdan:

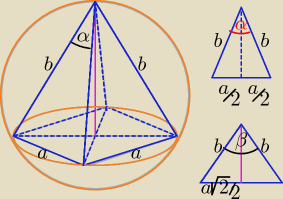
a   2		α		a
	= sin		⇒ b =
b		2		α   2sin   2

a√2   2		β		a√2		a		β		2
	= sin		⇒		=		* sin		/ *
b		2		2		α   2sin   2		2		a

	β   sin   2		β		α
√2 =		⇒ sin		= √2 sin
	α   sin   2		2		2

	β
cos		= √1 − sin2(β/2) = √1 − 2sin2(α/2) = √cosα
	2

	β		β		α
sinβ = 2sin		cos		= 2 * √2 sin		* √cosα
	2		2		2

R − długość promienia kuli opisanej na ostrosłupie i jednocześnie długość promienia okręgu opisanego na trójkącie o bokach a√2, b, b i kącie β między ramionami b.

	a√2		a√2
Korzystamy z twierdzenia sinusów:		= 2R ⇒ R =
	sinβ		2sinβ

	α
Wystarczy wstawić do wzoru na R w miejsce sinβ wyrażenie 2√2sin		√cosα.
	2