kw ana: wykres funkcji y= |x−2| przecina okrąg o: x2 + y2 −4x−4=0 w punktach A i B. c) oblicz pole figury F= F1 n ( część wspólna) F2 , jesli F1 = {(x,y): x ∊ R i x2 + y2 − 4x − 4 ≤0}, f2={(x,y): x ∊ R i y ∊ R i y≤ | x− 2|}

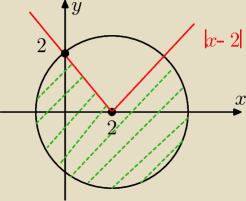
tom: x²+y²−4x−4=0 czyli (x−2)²+y²=8 F1 to koło o środku O=(2;0) promieniu r=2√2 F2 to "3/4" płaszczyzny poniżej wykresu y=|x−2| razem z tymi półprostymi część wspólna −na zielono (z brzegami). P=³₄ πr² = 6π