Witam. Robię sobie teraz zadania maturalne i nie potrafię zrobić kilku zadań. Prosze o pomoc
jakąś wskazówkę. Z góry dziękuję
Zad.1
Kwadrat o boku długości π rozcięto na dwa prostokąty, które po zwinięciu tworzą powierzchnie
dwóch walców o wysokości π. W jakiej odległości od jednego z boków należy dokonać cięcia
kwadratu, aby suma objętości walców w1 i w2 była najmniejsza?
Zad.2
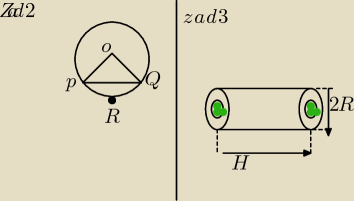
Przekrój poprzeczny tunelu metra o długości 3000m jest częścią koła o promieniu 4 m (rysunek).
Linia PQ wyznacza poziom tunelu, na którym będą ułożone szyny. Oblicz, ile metrów sześciennych
ziemi trzeba było usunąć, aby zbudować tunel. Do obliczeń przyjmij π ≈ 3,14.
Zad. 3
W stalowym walcu o wymiarach H= 4 dm, R= 6 cm, wydrążono cylindryczny otwór, którego objętość
stanowi 20% objętości całego walca. Oblicz:
a) długość promienia r tego otworu
b) masę walca po wydrążeniu, wiedząc że gęstość stali ρ= 7,9 g/cm3. Do obliczeń przyjij π≈
3,14 i wynik podaj z dokładnością do 0,1 kg. AD
| x | ||
2πr1 = x => r1 = | ||
| 2π |
| y | ||
2πr2 = y => r2 = | ||
| 2π |
| x2 | y2 | π2 − 2πy + 2y2 | ||||
V1 + V2 = π2*r12 + π2r22 = | + | = | = | |||
| 4 | 4 | 4 |
| 1 | 1 | π2 | |||
y2 − | πy + | − min. | |||
| 2 | 2 | 4 |
| −b | 1 | 1 | ||||
yw = | = U{ | π}{1 = | π | |||
| 2a | 2 | 2 |
| 1 | 1 | |||
y = | π x = | π | ||
| 2 | 2 |
Zad. 3 W stalowym walcu o wymiarach H= 4 dm, R= 6 cm, wydrążono cylindryczny otwór, którego
objętość stanowi 20% objętości całego walca. Oblicz: a) długość promienia r tego otworu b)
masę walca po wydrążeniu, wiedząc że gęstość stali ρ= 7,9 g/cm3. Do obliczeń przyjij π≈ 3,14 i
wynik podaj z dokładnością do 0,1 kg. AD
V = πR2*H = π*0,62 * 4 = 1,44π
Votworu = 20%* 1,44π = 0,288π
a)
0,288π = πr2H
0,288 = 4r2
0,072 = r2
| 3√5 | 6√5 | |||
r = | dm = | cm | ||
| 25 | 5 |
| m | ||
ρ = | ||
| V |
| 6√5 | 6 | |||
... | = | * √5 = 1,2 * √5  | ||
| 5 | 5 |
Ja juz dzisiaj nie mysle za duzo zadan zrobilam. Zostało tylko to 3 zad