Proszę o pomoc! Błagam! Okrąg w trójkącie! matma lovex: Takie zadanie męczy mnie pół wieczoru, i nie dam rady go zrobic Proszę o pomoc! W trójkącie równoramiennym ABC mamy dane: |AC|=|BC|=16cm oraz |AB|=12cm. W trójkąt ten wpisano okrąg. Oblicz długości odcinków, na jakie punkt styczności podzielił odcinek |AC|.

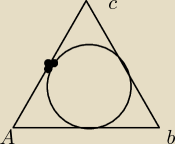matma lovex: To ma byc chyba cóś takiego jak na rysunku :

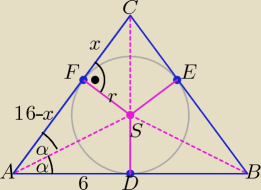Bogdan: Trójkąty ADS, ASF są przystające, 16 − x = 6 ⇒ x = 10.

matma lovex: Dziękuję bardzo za pomoc! Mam tylko jedno pytanie− udowodniłeś, że trójkąty ADS i ASF są przystające zgodnie z zasadą "bok kąt bok" ?

paziówna: x = 16 − y h − wys w trojkacie ABC h² = 16² − 6² = 256 − 36 = 220 h = √220 = 2√55 ΔCDO∼ΔGBC

r		6
	=
|CO|		16

|CO| = h − r

r		3
	=
2√55 − r		8

4r = 3(√55 − r) 7r = 3√55

	3√55
r =
	7

ΔCDO ∼ΔGBC

y		h
	=
r		6

6y = hr

	3√55
6y = 2√55*
	7

	55
y =
	7

	55		57
x = 16 −		=
	7		7

paziówna: x = 16 − y h − wys w trojkacie ABC h² = 16² − 6² = 256 − 36 = 220 h = √220 = 2√55 ΔCDO∼ΔGBC

r		6
	=
|CO|		16

|CO| = h − r

r		3
	=
2√55 − r		8

4r = 3(√55 − r) 7r = 3√55

	3√55
r =
	7

ΔCDO ∼ΔGBC

y		h
	=
r		6

6y = hr

	3√55
6y = 2√55*
	7

	55
y =
	7

	55		57
x = 16 −		=
	7		7

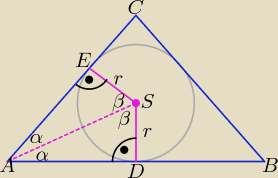Bogdan: Bok AS jest wspólnym bokiem dla trójkątów ADS i ASE, |DS| = |ES| = r. Środek okręgu wpisanego w trójkąt jest punktem przecięcia dwusiecznych kątów wewnętrznych, a więc miary kątów ADS i SAE są równe sobie, oznaczmy je α. Trójkąty ADS i ASE są prostokątne, więc miary kątów ASD i ASE są równe 90 − α, oznaczmy je β. Biorąc wymienione stwierdzenia pod uwagę ustalamy, że trójkąty ADS i ASE są przystające na podstawie cechy bkb.