zad
matthew:
Cześć,
mam takie zadanie:
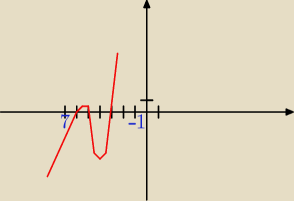
Wielomian f, którego fragment wykresu przedstawiono na rysunku spełnia warunek f(0) = 90.
Wielomian g dany jest wzorem g(x) = x
3 − 14x
2 +63x −90. Wykaż, że g(x) = − f(−x) dla x ∊R
Jak mam to wykazać?
Po prostu znależć miejsca zerowe g(x) i wykres przedstawić na tej samej osi co f(x) ?
Mam jeszcze takie zadanie:
ozwiąż równanie: 4cos
2x = 4sinx+1 w przedziale <0, 2π>
zrobiłęm tak:
4cos
2x = 4sinx+1
4(1−sin
2x) − 4sinx −1= 0
4 − 4sin
2x − 4sinx −1= 0
−4sin
2x − 4sinx + 3 = 0
t = sinx
−4t
2 − 4t +3 = 0
Δ = 64
√Δ = 8
brak rozwiązań
| | π | | 5 | |
Odp: x = |
| + 2kπ, x = |
| π + 2kπ |
| | 6 | | 6 | |
Bardo proszę o sprawdzenie i podpowiedź do zadania pierwszego
Z góry dziękuję
22 mar 19:14
matthew: Mam jeszcze takie zadanie:
| | √2 | |
Wyznacz dziedzinę i najmniejszą wartość funkcji: f(x) = log |
| (8x − x2) z tym, że |
| | 2 | |
| | √2 | |
|
| jest w indeksie dolnym logarytmu |
| | 2 | |
a>0 b>0
a≠0
x(−x +8)>0
x = 0 x = 8
x∊(−
∞,0)∪(8,+
∞)
Bardzo proszę o sprawdzenie...
Nie wiem jak zabrac sie za wartość....
22 mar 20:09
matthew: | | √2 | |
Ajć pomyliłem się przy tej dziedzinie. Jednak wyszło mi D = ( |
| ,8) |
| | 2 | |
Proszę o pomoc
22 mar 20:39
Jack:
1) z rysunku można odczytać punkty zerowe x=−6, −5, −3. Zatem nasza funkcja ma postać
f(x)=a(x+6)(x+5)(x+3)
Z tego że wiemy, że f(0)=90 wyliczymy a.
Potem należy wymnożyć te nawiasy i w ten sposób prosto już będzie wykazać, że g(x) = − f(−x) .
2) wg mnie ok
3) narysuj sobie wykres funkcji x(−x+8) i zauważ jak się zmienia monotoniczność tej funkcji
albo odczytaj ch−czne wartości tej funkcji i zobacz się zachowuje log dla tych wartości.
22 mar 20:49
matthew: Ok. dziekuję

wracając jeszcze do tego trzeciego zadania, dziedzina jest dobrze odczytana?
22 mar 20:52
Jack: W dziedzinie ramiona będą szły w dół... więc x∊(0,8).
22 mar 20:57
matthew: Tak sie zastanawiam nad tym pierwszym zadaniemi w sumie w dalszym ciągu nie wiem jak mam to
wykazać..... Zrobiłem wszystko, wyszło mi że f(X) = x3 +14x2+63x +90
Jak mam to wykazać....? Czy dowodem na to są te same miejsca zerowe o przeciwnych znakach?
mam narysować obydwa wykresy aby to udowodnić? NIe wiem... proszę o pomoc
22 mar 21:42
Jack: a wyjdzie 1 więc będziemy mieli f(x)=x3+14x2+63x+90 (o ile dobzre policzyłem)
zatem f(−x)=−x3+14x2−63x+90
stąd −f(−x)=x3−14x2+63x−90 = g(x)
22 mar 21:59
matthew: NIe wiem jak wyznaczyć tą wartość logarytmu....

NIe rozumiem, mam narysować parabolę x(−x+8)?
wtedy f. rosnąca byłaby dla x∊(−
∞,4) malejąca dla x∊(4, +
∞) .... Proszę o pomoc
22 mar 23:03
matthew: Mam jeszcze takie zadanie:
Liczby x1 = 5 +√23 i x2 = 5 − √23 są rozwiązaniami równania x2 −(p2 + q2)x + (p+q) =0
z niewaiadomą x. Oblicz wartości p i q
NIe wiem x1 i x2 to miejsca zerowe
Czy mam je podstawić do wzoru na postać iloczynową i obliczyć? współczynnik "a" to chyba 1....
Proszę o pomoc
22 mar 23:17
Tomek.Noah:
x
1 i x
2 to pierwiastki rownania tzn ze jak wstawisz pod miejsce x to ma ci wyjsc zero
a wiec x do rowania masz wtedy 2 rowania i 2 nie wiadome czy zadanie do zrobienia

22 mar 23:19
Godzio: z Vieta najlepiej
25 − 23 = p + q
10 = p
2 + q
2
2 = p+q
10 = p
2 + q
2
22 mar 23:19
matthew: Czyli jakbym zrobił tak: y = (x − 5 − √23)(5 − 5 +√23) = x2 − 10x + 2
wychodzi z tego że p2 + q2 = 10 oraz p + q = 2, ale czy to jest możliwe zeby coś do kwadratu
dodać coś do kwadratu wyszło 10 p i q muszą wynosić 1, 2 albo 0, ponieważ wynika
to z p + q = 2, ale w takim razie nie byłoby chyba mozliwe, aby z takich liczb podniesionych
do kwadratu wyszła dziesiątka..... wiecie o co mi chodzi...?
22 mar 23:26
matthew: możecie mi coś wiecej powiedziec na temat tego drugiego zadania z logarytmem, ponieważ nie
bardzo rozumiem to co napisał
Jack Dzieki za odpowiedzi

22 mar 23:27
Godzio:
czemu nie możliwe

?
p = 2−q
10 = (2−q)
2 + q
2
10 = 4 − 4q + 2q
2
2q
2 − 4q − 6 = 0
q
2 − 2q − 3 = 0
(q−3)(q+1) = 0
q = 3 v q = −1
q = 3 => p = −1
q = −1 => q= 3
22 mar 23:35
matthew: Ok. przekonałeś mnie

22 mar 23:49
matthew: Mam jeszcze takie zadanie:
W ostrosłu[pie prawidłowym czworokątnym dane są H − wysokość ostrosłupa oraz α − miara kąta
utworzonego przez krawędź boczną i krawędź podstawy (45
o<α>90
o).
| | 4 | | H3 | |
Wykaż, ze objętość V tego ostrosłupa jest równa |
| * |
| |
| | 3 | | tg2α−1 | |
Zrobiłem tak:
| 4 | | H3 | | PpH | |
| * |
| = |
| / *3 |
| 3 | | tg2α−1 | | 3 | |
| | 1 | | 4H2 | | 4H3 | | 4 | | H3 | |
V = |
| * |
| * H = |
| = |
| * |
| |
| | 3 | | tg2α−1 | | 3(tg2α−1) | | 3 | | tg2α−1 | |
NIe jestem pewny czy to ma właśnie tak wyglądać... proszę o pomoc
23 mar 00:23
Jack: Z tego co widzę zacząłeś rozwiązywać zadanie, zakładając to do czego masz dopiero dojść! Czemu
zaraz po napisaniu wzoru na objętość piszesz:
| 4 | | H3 | |
| * |
| =.... ? Skąd to wiesz  |
| 3 | | tg2α−1 | |
23 mar 00:26
matthew: ok to moment bo chyba wiem jak to znaleźć
23 mar 00:30
matthew: tylko mam pytanie, ile w końcu wynosi α
23 mar 00:31
Debek : Możecie zerknąć na moje zadanie ?
23 mar 00:31
matthew: tam powinno być<45o<x<90o>
23 mar 00:32
matthew:
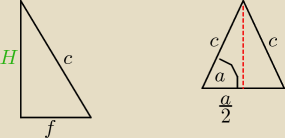
Zacząłem tak...
c =
√H2 + 12a2
i dalej nie wiem, bo nie wiem ile wynosi α <45
o<α<90
o>....
23 mar 00:53
Jack:
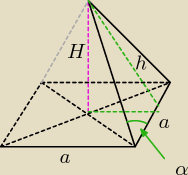
| | d*√2 | |
1. W podstawie mamy kwadrat więc przekątna d ma wzór d=a√2 ⇒a= |
|
|
| | 2 | |
zatem
z Tw. Pit.:
| | 2h | |
Pole podstawy: Pp=a2=( |
| )2=
|
| | tgα | |
| | H2*tg2α | | 1 | | H2 | |
=4 |
| * |
| =4 |
|
|
| | tg2α−1 | | tg2α | | tg2α−1 | |
23 mar 01:02
Jack: ta uwaga o przekątnej w podstawie jest oczywiście zbędna − to wynik wcześniejszych prób

23 mar 01:03
matthew: ok dzieki
mam jeszcze jedno zadanie:
| | 2 | |
Dane jest równanie | |
| + 3| = p z niewiadomą x. Wyznacz liczbę rozwiązań tego równania w |
| | x | |
zależności od parametru p. proszę o pomoc
23 mar 01:27
krokus:
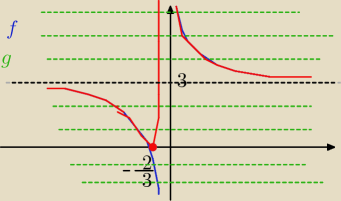
| | 2 | |
f(x) = I |
| +3I −−− czerwony wykres
|
| | x | |
g (x)= p −−− zielone wykresy
dla p€( −∞, 0) −−− brak rozwiązań
dla p=0 v p=3 −−− 1 rozwiązanie
dla p€( (0, 3) U ( 3 , ∞) −−− 2 rozwiązania
23 mar 01:45
Mateusz: W zadaniu 1 troche sie pospieszyliscie bo nie jest napisane o jaki wielomian chodzi tzn jakiego
stopnia załozyliscie ze chodzi o wielomian 3 −go stopnia to ma wynikac z tresci zadania
inaczej jest takich wielomianów nieskonczenie wiele.
23 mar 08:59
Jack: z rys "widać" że jest trzeciego. Po pierwsze, gdyby było inaczej rysunek, byłby bezużyteczny.
Po drugie dlatego, że gdyby mógł być innego stopnia, nie do udowodnienia byłaby równość
g(x)=−f(−x).
23 mar 19:20
23 mar 21:52
 Cześć,
mam takie zadanie:
Wielomian f, którego fragment wykresu przedstawiono na rysunku spełnia warunek f(0) = 90.
Wielomian g dany jest wzorem g(x) = x3 − 14x2 +63x −90. Wykaż, że g(x) = − f(−x) dla x ∊R
Jak mam to wykazać?
Po prostu znależć miejsca zerowe g(x) i wykres przedstawić na tej samej osi co f(x) ?
Mam jeszcze takie zadanie:
ozwiąż równanie: 4cos2x = 4sinx+1 w przedziale <0, 2π>
zrobiłęm tak:
4cos2x = 4sinx+1
4(1−sin2x) − 4sinx −1= 0
4 − 4sin2x − 4sinx −1= 0
−4sin2x − 4sinx + 3 = 0
t = sinx
−4t2 − 4t +3 = 0
Δ = 64
√Δ = 8
Cześć,
mam takie zadanie:
Wielomian f, którego fragment wykresu przedstawiono na rysunku spełnia warunek f(0) = 90.
Wielomian g dany jest wzorem g(x) = x3 − 14x2 +63x −90. Wykaż, że g(x) = − f(−x) dla x ∊R
Jak mam to wykazać?
Po prostu znależć miejsca zerowe g(x) i wykres przedstawić na tej samej osi co f(x) ?
Mam jeszcze takie zadanie:
ozwiąż równanie: 4cos2x = 4sinx+1 w przedziale <0, 2π>
zrobiłęm tak:
4cos2x = 4sinx+1
4(1−sin2x) − 4sinx −1= 0
4 − 4sin2x − 4sinx −1= 0
−4sin2x − 4sinx + 3 = 0
t = sinx
−4t2 − 4t +3 = 0
Δ = 64
√Δ = 8
 wracając jeszcze do tego trzeciego zadania, dziedzina jest dobrze odczytana?
wracając jeszcze do tego trzeciego zadania, dziedzina jest dobrze odczytana?
 NIe rozumiem, mam narysować parabolę x(−x+8)?
wtedy f. rosnąca byłaby dla x∊(−∞,4) malejąca dla x∊(4, +∞) .... Proszę o pomoc
NIe rozumiem, mam narysować parabolę x(−x+8)?
wtedy f. rosnąca byłaby dla x∊(−∞,4) malejąca dla x∊(4, +∞) .... Proszę o pomoc


 ?
p = 2−q
10 = (2−q)2 + q2
10 = 4 − 4q + 2q2
2q2 − 4q − 6 = 0
q2 − 2q − 3 = 0
(q−3)(q+1) = 0
q = 3 v q = −1
q = 3 => p = −1
q = −1 => q= 3
?
p = 2−q
10 = (2−q)2 + q2
10 = 4 − 4q + 2q2
2q2 − 4q − 6 = 0
q2 − 2q − 3 = 0
(q−3)(q+1) = 0
q = 3 v q = −1
q = 3 => p = −1
q = −1 => q= 3


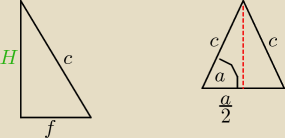 Zacząłem tak...
Zacząłem tak...


