ciagi arytmetyczne Sara: Pomocy! Wykaz, ze dlugosci bokow trojkata prostokatnego tworza ciag arytmetyczny wtedy i tylko wtedy, gdy trojkat ten jest podobny do trojkata o bokach 3, 4, 5. Bardzo prosze o jak najszybsza pomoc. !

paziówna: ja sprobuje

Sara: Prosze o pomoc Kochani

paziówna: mi nie idzie:(

Anna: pomogę

paziówna: tzn moge "<=" 3t, 4t, 5t t∊ℕ ciag arytm(boki trojkata)

	3t+5t
4t =		= 4t
	2

prawda

Jack: a ponad to zachowujemy prostokątność bo (3t)²+(4t)²=(5t)² 25t²=25t² L=P

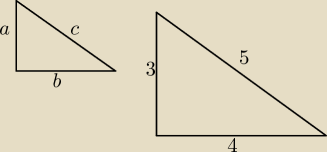
Anna: k − skala podobieństwa trójkątów Czyli: a = 3k, b = 4k, c = 5k Należy wykazać, że ciąg: (a, b, c) = (3k, 4k, 5k) jest arytmetyczny. Wystarczy sprawdzić własność ciągu:

	3k + 5k
4k =
	2

L = 4k

	8k
P =		= 4k
	2

L = P c.n.d.

Jack: "ponadto"

Sara: Tyle to ja tez zrobilam tylko czy to Wszystko

Sara: Dzieki

paziówna: to nie wszystko. trzeba udowodnic w druga strone. tzn majac trojkat o bokach tworzacych ciag arytmetyczny to ten trojkat jest podobny do tr o bokcach 3,4,5

b.: zalozmy ze mamy trojkat o bokach dlugosci a−r, a, a+r (czyli tworzacych ciag arytmetyczny), ktory to trojkat jest prostokatny wtedy z tw. Pitagorasa (przeciwprostokatna jest najdluzszy bok, czyli a+r): (a−r)² + a² = (a+r)² i stad a² = 4ar poniewaz a≠0, wiec a = 4r zatem dlugosci bokow to 4r−r=3r, 4r, 4r+r=5r, wiec jest to trojkat podobny do trojkata ... 3,4,5