
 o ile moje obliczenia sa dobre.
o ile moje obliczenia sa dobre.
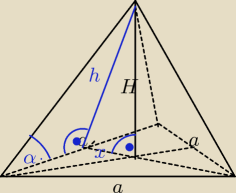
| 1 | a2√3 | |||
Dane: h, α , V = ? V = | * | * H | ||
| 3 | 4 |
| h | ||||||||
= tgα | ||||||||
|
| a | h | 1 | 1 | a√3 | √3 | 2h | ||||||||
= | x = | hp = | * | = | * | |||||||||
| 2 | tgα | 3 | 3 | 2 | 6 | tgα |
| 2h | h√3 | |||
a = | = | |||
| tgα | 3tgα |
| h√3 | ||
H2 + ( | )2 = h2 | |
| 3tgα |
| 3h2 | ||
H2 = h2 − | ||
| 9tg2α |
| h2 | ||
H2 = h2 − | ||
| 3tg2α |
| 3h2tg2α − h2 | ||
H2 = | ||
| 3tg2α |
| h2(tg2α − 1) | ||
H2 = | ||
| 3tg2α |
| h√tg2α−1 | h√3*√tg2α − 1 | |||
H = | = | |||
| √3tgα | 3tgα |
| 1 | 2h | h√3*√tg2α−1 | ||||
V= | * ( | )2*√3* | = | |||
| 12 | tgα | 3tgα |
| 4h3*3√tg2α−1 | h3√tg2α−1 | |||
= | = | |||
| 12tg2α * 3tgα | tg3α |


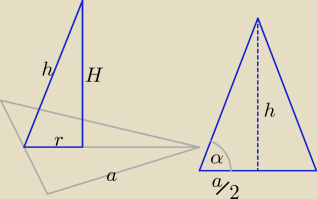 Dobry wieczór.
Anno, mam nadzieję, że nie pogniewasz się, jeśli przedstawię tę wersję rozwiązania.
Dobry wieczór.
Anno, mam nadzieję, że nie pogniewasz się, jeśli przedstawię tę wersję rozwiązania.
| ||||||||||
= ctgα ⇒ a = 2h*ctgα | ||||||||||
| h |
| 1 | 1 | 2 | ||||
r = | a√3 = | *2h*ctgα*√3 = | *h*ctgα | |||
| 6 | 3 | √3 |
| 4 | 4 | |||
H2 = h2 − r2 = h2 − | h2*ctg2α = h2(1 − | *ctg2α) | ||
| 3 | 3 |
| √3 − 4ctg2α | ||
H = h* | ||
| √3 |
| 1 | 1 | √3 − 4ctg2α | 1 | |||||
V = | * | *4h2*ctg2α*√3*h* | = | h3*ctg2α√3 − 4ctg2 | ||||
| 3 | 4 | √3 | 3 |