ważne gimigis: hej mam parę pytań związanych z funkcjami logarytmicznymi: 1. mam takie zadanko: f(x) = log_0,1 (x² − 1) i muszę wyznaczyć dziedzinę i mi nie wychodzi (x²−1) > 0 (x−1)(x+1)>0 x>−1 v x>1 i według mnie powinno być: x∊(1,∞) a w odpowiedzi jest, że D = (−∞,−1) u (1,∞) Dlaczego 2. kolejne zadanie: f(x) = log₂ [x−1] klamerki to wartość bezwzględna i mam określić przedziały monotoniczności,narysowałam tą funkcję,chciałam określić te przedziały a w książce jest, że funkcja rośnie (1,∞) a maleje (−∞,1),skąd ta jedynka 3. i chciałam jeszcze zapytać,czyja jak mam wyznaczyć dziedzinę i zbiór wartości i mam na przykład taką funkcję:f(x) = log₃(x+3) −1 to dziedzina będzie (−3,∞) a zbiór wartości (−1,∞)

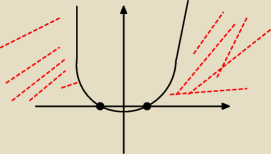
Lachu: podpowiem Ci w zadaniu pierwszym ze tak sie nie rozwiazuje z tego (x−1)(x+1)>0 malujesz funkcje cyzli jest wieksza od (−∞; −1)U(1;+∞)

gimigis: nie rozumiem... dlaczego nie mogę zrobić tak jak napisałam

godzio pomożesz?: https://matematykaszkolna.pl/forum/44307.html

Godzio: to jest wzór skróconego mnożenia albo można też tak ale tu sie czesciej bledy robi x² > 1 x > 1 v x < −1 x∊(−∞, −1)U(1,∞)

godzio pomożesz?: nio ja właśnie zastosowałam wzrór skróconego mnożenia...ale inaczej mi wyszło

godzio pomożesz?: jesteś

Godzio: (x−1)(x+1) > 0 zaznaczasz miejsca zerowe i sprawdzasz dla jakich x funkcja jest wieksza od zera

godzio pomożesz?: miejsce zerowe wychodzi x = −√2 i x = √2...powiedz mi co zrobiłam źle w tym moim zapisie

Godzio: 1 i −1 a nie √2

godzio pomożesz?: nie ma być √2,tak mi wyszło i taka jest odpowiedź w książce

Godzio: ale o którym my mówimy ?

Nikka: Zad. 1 − liczba logarytmowana to funkcja kwadratowa, rozwiązując nierówność kwadratową szukamy pierwiastków (tu łatwo się odczytuje bo jest zapisana w postaci czynnikowej) i rysujemy wykres paraboli a następnie sprawdzamy gdzie przyjmuje wartości dodatnie − ramiona są skierowane do góry, 1.−1 to pierwiastki, więc rozwiązaniem jest suma przedziałów x∊(−∞,−1)∪(1,∞).

godzio pomożesz?: o zadaniu pierwszym,widzisz go? mi cały czas tylko chodzi o tą dziedzinę

Godzio: (x²−1) > 0 (x−1)(x+1)>0 x<−1 v x>1

godzio pomożesz?: dlaczego

Godzio: tak to juz jest x² > 1 /√ |x| > 1 x>1 v x<−1 tak sie rozwiazuje

Nikka: sama napisałaś, że odp. w zad. 1 to (−∞, −1)∪(1,∞) i nie wiesz dlaczego, to może się zdecyduj jaka w końcu jest ta odpowiedź? albo sprawdź wzór funkcji ...

godzio pomożesz?: odpowiedź jest taka jak napisałam,na nic nie muszę się decydować, nie rozumiem tej pierwszej części odpowiedzi (−∞,−1) możesz mi odpowiedzieć Godzio na 3 pytanie

godzio pomożesz?: ale miejsce zerowe dobrze mi wyszło w tym pierwszym

Godzio: ja juz nie mam pojecia o co chodzi

godzio pomożesz?: poczekaj...musimy to uporządkować cały czas mówiliśmy o zadaniu pierwszym. Miejsce zerowe wyznaczyłam bez problemu wyszło mi √2 lub −√2. Nie rozumiałam tylko dziedziny,ale mniejsza o to już Teraz pytam się o zadanie 3

Nikka: y = x² −1 = (x−1)(x+1) − funkcja kwadratowa − rysujemy wykres paraboli , a=1>0 − ramiona do góry, −1, 1 − miejsca zerowe

godzio pomożesz?: to są logarytmymiejsce zerowe ma być √2 lub −√2,tak mi wyszło i taka jest odpowiedź w książce,nie wracajmy już do tych miejsc zerowych bo nie o to mi chodzi,napisałam już,że miejsca wyznaczyłam bez problemu...

Nikka: Wykres jest narysowany wyżej przez Lachu, D = (−∞, −1) ∪ (1,∞) log_0,1(x²−1) = 0 log_0,1(x²−1) = log_0,11 x² − 1 = 1 x² −2 = 0 x = √2 lub x = −√2 tylko jakie było polecenie − bo jeśli wyznaczyć tylko dziedzinę to po co liczyć miejsca zerowe funkcji...

godzio pomożesz?: chcieli miejsca i dziedzinę

godzio pomożesz?: odpowiecie na pytanie 3