pomocy kiełbasa: wyznaczyć ekstremum funkcji: F(x)=√3−sin2x, x∊(0,π) co robię źle? 1. D_f=R 2. f'(x)=√3−2cos2x 3. D_f=D_f' 4. f'(x)=0⇔√3−2cos2x=0

	π		π
x=		+kπ v x=−		+kπ
	12		12

	π		11
x=		v x=		π
	12		12

do tego momentu wszystko jest dobrze, problem zaczyna się gdy muszę namalować sgn f'(x) i określić min i max sądziłam, że mogę potraktować to jako fragment wykresu funkcji cos2x, ale tak nie jest, ponieważ potem z mojego wykresu wynika, że max znajduje się tam, gdzie w rzeczywistości (jak podają odpowiedzi) ma być min i na odwrót. proszę o pomoc, ewentualny rysunek. mimo chęci nie załącza mi się mój obrazek

Edek: błąd popełniasz przy wyznaczaniu pochodnej funkcji f'(x)=−2cos2x, gdyż pochodna ze stałej √3 wynosi 0, spróbuj teraz rozwiązać zadanie

kiełbasa: Edku, dziękuję za odpowiedź, jednak błąd który znalazłeś był w tym, że źle przepisałam tutaj funkcję wyjściową, która miała wyglądać tak: f(x)=√3x−sin2x a więc pochodna jest dobrze wyznaczona. Generalnie problem mój tkwi w tym, że nie umiem namalować wykresu pochodnej, nie wiem od której strony zacząć rysowanie i w ogóle jak się do tego brać.

Edek: a więc, co do wykresu 1. Narysuj wykres cosx 2. Narysuj cos(2x) dla argumentu 2x , tzn. dla 0<a<1 będzie się rozszerzał, dla a>1 będzie się zwężał, w naszym przypadku mamy a=2, czyli będzie się zwężał, np.

	π
mieliśmy dla przy π minimum (górkę na dole) teraz będziemy mieli przy
	2

3. Narysuj 2cos(2x), tzn. powiększ wartości twojej funkcji, w tym przypadku o 2,np. wykres cosx miał przedział <−1,1> , wykres 2cosx będzie miał przedział <−2,2> 4. Odbij wykres o oś X, czyli symetria osiowa względem osi OX, do otrzymania −2cos(2x) 5. Na końcu dodaj √3 do wartości twojej funkcji, czyli do przedziału <−2,2>, otrzymamy <−2+√3 , 2+√3 > 6. Sporządź wykres

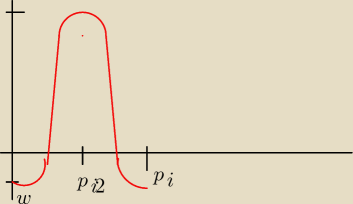
Edek: wykres coś do tego podobny

kiełbasa:

	1		1
dziękuję, wyznaczyć ekstremum funkcji: 2.50c) f(x)=		x5−		x4−x3+2x2+4x−7
	5		2

postępuję analogicznie: 1.D=R 2.f'(x)=x⁴−2x³−3x²+4x+4 3.x⁴−2x³−3x²+4x+4=0⇔x=−1(IIkr.) v x=2( I krotny)

	3
z tabeli, którą sporządziłam wynika że f. mam max lokalne w fmax(2)=−
	5

odpowiedzi mówią że nie ma ekstremum. Gdzie robię błąd? Proszę o poprawne rozwiązanie.

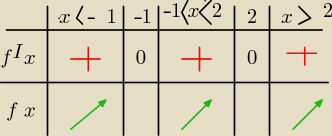
Edek: funkcja nie będzie mieć ekstremów, gdyż f'(x)=(x+1)²(x−2)² miejscami zerowymi są x=−1 oraz x=2, ale funkcja f'(x) > 0 → x ∊ R f'(x) < 0 → x∊ zbiór pusty i widzimy, że funkcja nie zmienia znaku, czyli nie przechodzi z malejącej na rosnącą lub na odwrót, wówczas nie ma mowy o ekstremum funkcji ( warunek wystarczający )