? Haaaaaaanka: (x−2)(x+5)≥0

Cinu: https://matematykaszkolna.pl/strona/93.html

Haaaaaaanka: no dobrze ale po rozwiazaniu wychodzi: (x−2)≥0 (x+5)≥0 x≥ 2 x ≥ −5 i po wykonaniu rysunku wspolną czescią jest przedział <−5;2> a wiem ze wynik musi byc: (−∞,−5> ∪ <2, ∞) Czy mogłby ktoś poprawnie wykonać ten przykład?

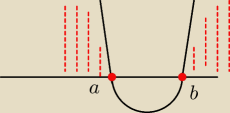
Jack: a=−5 b=2 Szukamy przedziałów, dla których wykres leży nad osią OX (przyjmuje wartości niemniejsze od 0).

Cinu: to źle podpowiedzialem?

Jack: przepraszam, nie sprawdziłem Twojego odnośnika − faktycznie wszystko jest w nim zawarte. Nie potrzebnie robiłem rysunek... Przynajmniej odpowiedzi nie napisałem Nie wiem skąd bierzesz część wspólną obu przedziałów, Haaaaanko.

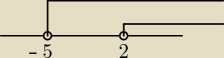
Haaaaaaanka: nie rozumiem matmy jestem w 2 gimn i nie mam zielonego pojecia o tym, a nie rzoumiem poniewaz uczyliśmy sie w ten sposób, że patrzy się na to w którą stornę skierowany "jest dziubek" −−> tak wiem, wrecz smieszne nauczanie ale tak nam mowiono, a patrząc po tym wychodzi tak: x≥2 x≥−5

Cinu: x≥2 wiec wiadomo ze jest tez wieksze od −5, masło maślane

Cinu: https://matematykaszkolna.pl/forum/44249.html << proszę o pomoc!

Nikka: podana nierówność jest nierównością kwadratową (nie rozbijamy jej na dwie nierówności) − pierwiastki można łatwo odczytać bo funkcja zapisana jest w postaci czynnikowej : x = 2 lub x = −5 Sprawdzamy a czyli współczynnik przed x²(jest dodatni, więc ramiona paraboli do góry) i rysujemy wykres paraboli tak jak to zrobił Jack. Sprawdzamy gdzie funkcja przyjmuje wartości dodatnie i równe 0 (część wykresu nad osią OX łącznie z miejscami zerowymi). Rozwiązaniem jest suma przedziałów (−∞, −5>∪<2,∞)

Haaaaaaanka: juz rozumiem, dzikuje

Nikka: A jeśli już chcesz z jakiś powodów rozbić na nierówności to powinno być: ( x−2≥0 i x+5≥0 ) lub ( x−2≤0 i x+5 ≤0 ) [wynik mnożenia obu nawiasów ma być dodatni (czyli albo oba nawiasy są liczbami dodatnimi albo liczbami ujemnymi bo iloczyn dwóch liczb ujemnych daje liczbą dodatnią) bądź równymi zero...] najpierw wyznaczmy części wspólne z nawiasów, a następnie wyniki sumujemy (lub=suma), wynik będzie dokładnie taki sam...