 W układzie współrzędnych zilustruj zbiór punktów, których współrzędne
spełniają równanie logx2 + y2 (2y) = 1
W układzie współrzędnych zilustruj zbiór punktów, których współrzędne
spełniają równanie logx2 + y2 (2y) = 1
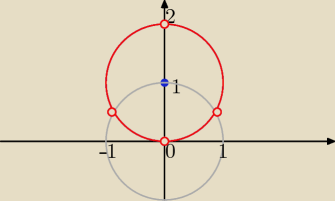 założenie: y >0 i x2+y2 >0 => x ≠0 i y≠0 i x2+y2 ≠1
z def log: (x2+y2)1= 2y => x2+y2−2y=0 => x2+( y−1)2= 1
mamy okrąg o środku S(0,1) i r= 1
teraz tylko jego punkty muszą spełniać założenia
ten czerwony okrąg z "dziurkami" −−− to właśnie zbiór tych punktów
spełniających to równanie
szary okrąg podstawa x2+y2 ≠ 1
założenie: y >0 i x2+y2 >0 => x ≠0 i y≠0 i x2+y2 ≠1
z def log: (x2+y2)1= 2y => x2+y2−2y=0 => x2+( y−1)2= 1
mamy okrąg o środku S(0,1) i r= 1
teraz tylko jego punkty muszą spełniać założenia
ten czerwony okrąg z "dziurkami" −−− to właśnie zbiór tych punktów
spełniających to równanie
szary okrąg podstawa x2+y2 ≠ 1
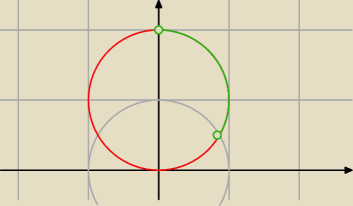 zielone to rozwiązanie
zielone to rozwiązanie