ostrosłup i kula kasia: Wysokość trójkątnego ostrosłupa prawidłowego ma długość h, a krawędzie boczne są do siebie prostopadłe. Wyznacz długość promienia kuli opisanej na tym ostrosłupie. Proszę o pomoc, rysunek, bo nawet nie umiem sobie tego wyobrazić

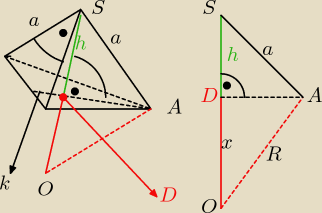
tom: prawidłowy tzn podstawa jest Δ równobocznym o boku =a√2(przeciwprostokątna Δ prostokątnego

	(a√2)√3		2		√2
równoramiennego) wysokość podstawy k=		|DA|=		k=a
	2		3		√3

	2a2
z ΔSAD a2 = h2 + |DA|2 a2 = h2 +		a=√3h |DA|2 = a2 − h2
	3

po podstawieniu |DA| = h√2 środek kuli leży na prostej zawierającej wysokość ostrosłupa ozn. przez O , R promień, więc R=h+x

	3
z ΔAOD (h+x)2 = x2 + |DA|2 ; h2+2h+x2=x2+2h2 ; 2x=h R=		x
	2