ss Basia ;): Bardzo proszę o pomoc w takim przykładzie

1+x		1−2x
	<		−1
1+2x		x+1

Proszę o jakąkolwiek pomoc

R.W.16l:

1+x		1−2x
	−		< −1
1+2x		x+1

(1+x)(x+1)		(1−2x)(1+2x)
	−		< −1
(1+2x)(x+1)		(x+1)(1+2x)

x2+2x+1		1−4x2
	−		< −1
x+1+2x2+2x		x+1+2x2+2x

x2+4x2+2x+1−1
	< −1
x+1+2x2+2x

5x2+2x
	< −1
2x2+3x+1

5x²+2x < −2x²−3x−1 7x²+5x+1 < 0 7x²+5x < −1 x(7x+5) < −1 iloczyn dwóch liczb jest ujemny tylko gdy jedna jest dodatnia a druga ujemna x<0 x>0 7x+5>0 lub 7x+5<0 x<0 x>0

	5		5
x>−		lub x<−
	7		7

trochę dziwne, czyli źle pewnie ale skoro się napracowałem to wyślę... btw. wczesniej było tego dwa razy więcej ale usunąłem więc się napracowałem wiecej pozdr

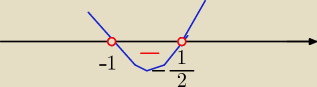
abc: założenie: 1+2x≠0 i x+1 ≠0 => x≠−¹₂ i x ≠ −1 wspólny mianownik: (1+2x)(x+1)

	(1+x)*(x+1) −(1−2x)(1+2x) +1(1+2x)(x+1)
		<0
	(1+2x)(x+1)

	(x+1)2 −( 1−4x2) + 1+3x+2x2
		<0
	(1+2x)(x+1)

po uporządkowaniu licznika otrzymasz:

7x2+5x+1
	<0
(1+2x)(x+1)

dla 7x²+5x+1 Δ<0 −−− więc to wyrażenie jest zawsze dodatnie dla x€R pozostaje zatem: ułamek < 0 , wtedy gdy mianownik <0 , bo licznik zawsze >0 (1+2x)(x+1) <0 odp: x€( −1, −¹₂)

Basia ;): Dziękuję bardzo

abc: Komu dziękujesz? ....... bo R.W.16 coś "pokićkał"

Basia ;): oczywiście że Tobie xD

R.W.16l: ej no

R.W.16l: pisz się R.W.16l a nie R.W.16