zadanie MIchał: Mam problem z tym zadaniem Obliczyć objętość czworościanu foremnego o krawędzi długości a. Udowodnić, że jeżeli punkt należy do wnętrza czworościanu foremnego, to suma jego odległości od ścian tego czworościanu jest stała.

tom:

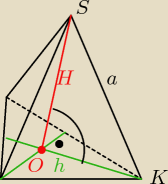
	√3
wysokość ścian h= a		; wysokości w Δ równobocznym przecinają sie w stosunku 2:1; z
	2

	2		4		3
ΔSKO można wyznaczyć wysokość H czworościanu H2= a2 − (		h)2 =a2(1−		*		) =
	3		9		4

	2a2		√2		1	a2√3		√2		a3√2
		H=a		V= PpH =			a		=
	3		√3		3	4		√3		12

tom: cz. 2 . można tak uzasadnić : − pkt wewnętrzny W czworościanu połączyć z wierzchołkami − powstaną wtedy 4 ostrosłupy − podstawy są jednakowe (ściany czworościanu) − suma obj. ostrosłupów jest równa obj. czworościanu − ich wysokości to odległości W od ścian czworościanu, a ich suma wynosi H

	1
( gdyby to liczyć to przed nawias wyłączy sie		PP w nawiasie pozostanie h1+....h4)
	3

mariano: Δ

mariano: nie ma za co

mariano: ∊ΩΔπδγβα∞≤∊

mariano: saturn